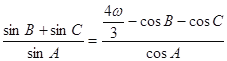题目内容
【题目】若存在实数![]() ,对任意实数
,对任意实数![]() ,使不等式
,使不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围为________.
的取值范围为________.
【答案】![]()
【解析】
不等式![]() 可化为不等式
可化为不等式![]() ,等价于存在实数a,b,对任意
,等价于存在实数a,b,对任意![]() ,不等式
,不等式![]() 成立,等价于存在实数a,b,不等式
成立,等价于存在实数a,b,不等式![]() 成立,分别讨论
成立,分别讨论![]() ,
,![]() ,
,![]() 的情况,注意由任意性和存在性可知需先求出
的情况,注意由任意性和存在性可知需先求出![]() ,再求
,再求![]() 即可解决.
即可解决.
不等式![]() 可化为不等式
可化为不等式![]() ,
,
原题等价于存在实数a,b,对任意![]() ,不等式
,不等式![]() 成立,
成立,
等价于存在实数a,b,不等式![]() 成立,
成立,
令![]() ,则
,则![]() ,
,
(1)在![]() 上,当
上,当![]() ,即
,即![]() 时,函数单调递减,
时,函数单调递减,
此时![]() ,
,
当![]() 时,
时,![]() ,且
,且![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,且
,且![]() ,则
,则![]() ,
,
从而当![]() 时,设
时,设![]() ,
,
则![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
所以![]() 时,
时,![]() 取最小值,最小值为
取最小值,最小值为![]() ;
;
(2)当![]() 时,由
时,由![]() 可得,y在
可得,y在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
①在![]() 时,
时,![]() ,则
,则![]() ,
,
同理可得,当![]() 时,
时,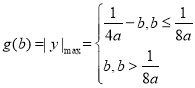 ,则
,则![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,故当
单调递增,故当![]() 时,
时,![]() 取最小值,最小值为
取最小值,最小值为![]() ;
;
②在![]() 时,
时,![]() ,则
,则![]() ,
,
同理可得,当![]() 时,
时,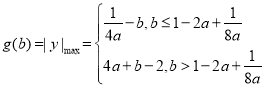 ,则
,则![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
故当![]() 时,
时,![]() 取最小值,最小值为
取最小值,最小值为![]() ,
,
根据对勾函数的性质可得,![]() .
.
综上所述,![]() ,即
,即![]() ,
,![]() .
.
故答案为:![]() .
.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
【题目】某校高三的某次数学测试中,对其中100名学生的成绩进行分析,按成绩分组,得到的频率分布表如下:
组号 | 分组 | 频数 | 频率 |
第1组 | [90,100) | 15 | ① |
第2组 | [100,110) | ② | 0.35 |
第3组 | [110,120) | 20 | 0.20 |
第4组 | [120,130) | 20 | 0.20 |
第5组 | [130,140) | 10 | 0.10 |
合计 | 100 | 1.00 |
(1)求出频率分布表中①、②位置相应的数据;
(2)为了选拔出最优秀的学生参加即将举行的数学竞赛,学校决定在成绩较高的第3、4、5组中分层抽样取5名学生,则第4、5组每组各抽取多少名学生?