题目内容
已知二次函数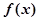 满足:①在
满足:①在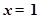 时有极值;②图像过点
时有极值;②图像过点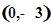 ,且在该点处的切线与直线
,且在该点处的切线与直线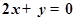 平行.
平行.
(1)求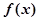 的解析式;
的解析式;
(2)求函数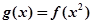 的单调递增区间.
的单调递增区间.
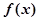 满足:①在
满足:①在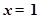 时有极值;②图像过点
时有极值;②图像过点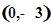 ,且在该点处的切线与直线
,且在该点处的切线与直线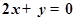 平行.
平行.(1)求
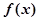 的解析式;
的解析式;(2)求函数
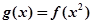 的单调递增区间.
的单调递增区间.(1)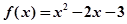 ;(2)函数
;(2)函数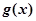 的单调递增区间为(-1,0),(1,+∞).
的单调递增区间为(-1,0),(1,+∞).
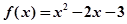 ;(2)函数
;(2)函数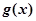 的单调递增区间为(-1,0),(1,+∞).
的单调递增区间为(-1,0),(1,+∞).试题分析:(1)根据题意首先设出该二次函数的解析式,然后根据题意列出方程组即可求出其解析式;
(2)直接运用导数研究函数
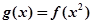 的单调性及单调区间.
的单调性及单调区间.试题解析:(1)设
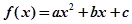 ,则
,则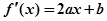 .
. 由题设可得:
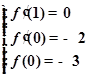 即
即 解得
解得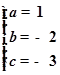
所以
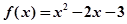 .
.(2)
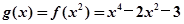 ,
,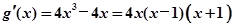 .
.列表:
| x | (-∞,-1) | -1 | (-1,0) | 0 | (0,1) | 1 | (1,+∞) |
 | - | 0 | + | 0 | - | 0 | + |
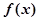 | ↘ | | ↗ | | ↘ | | ↗ |
由表可得:函数
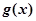 的单调递增区间为(-1,0),(1,+∞).
的单调递增区间为(-1,0),(1,+∞). 
练习册系列答案
相关题目
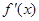 ,且满足
,且满足 ,则
,则 与
与 的大小关系为( ).
的大小关系为( ).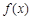 ,若对任意
,若对任意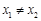 ,都有
,都有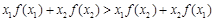 ,则称f(x)为“H函数”,给出下列函数:①
,则称f(x)为“H函数”,给出下列函数:①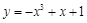 ;②
;② ;③
;③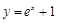 ;④
;④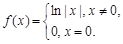 其中是“H函数”的个数为
其中是“H函数”的个数为
 若当0
若当0 时,
时, 恒成立,则实数m的取值范围是 ( )
恒成立,则实数m的取值范围是 ( )
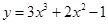 在区间
在区间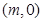 上为减函数, 则
上为减函数, 则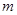 的取值范围是__ ___.
的取值范围是__ ___. 内不是增函数的是( )
内不是增函数的是( )



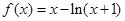 的减区间是 .
的减区间是 .