Question

【题目】已知四棱锥P﹣ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC= ，AB=1，M是PB的中点．

（1）证明：面PAD⊥面PCD；
（2）求AC与PB所成的角；
（3）求面AMC与面BMC所成二面角的大小余弦值．

Answer 1

【答案】
（1）证明：∵PA⊥面ABCD，CD⊥AD，

∴由三垂线定理得：CD⊥PD．

因而，CD与面PAD内两条相交直线AD，PD都垂直，

∴CD⊥面PAD．

又CD面PCD，

∴面PAD⊥面PCD．

（2）解：过点B作BE∥CA，且BE=CA，

则∠PBE是AC与PB所成的角．

连接AE，可知AC=CB=BE=AE= ，又AB=2，

所以四边形ACBE为正方形．由PA⊥面ABCD得∠PEB=90°

在Rt△PEB中BE=a2=3b2，PB= ，

∴cos∠PBE= ．

∴AC与PB所成的角为arccos ．

（3）解：作AN⊥CM，垂足为N，连接BN．

在Rt△PAB中，AM=MB，又AC=CB，

∴△AMC≌△BMC，

∴BN⊥CM，故∠ANB为所求二面角的平面角

∵CB⊥AC，由三垂线定理，得CB⊥PC，

在Rt△PCB中，CM=MB，所以CM=AM．

在等腰三角形AMC中，ANMC= ，

∴AN= ．

∴AB=2，

∴cos∠ANB= =﹣

故面AMC与面BMC所成二面角的大小余弦值为﹣ ．

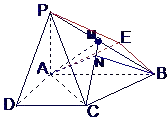
【解析】（1）证明面PAD⊥面PCD，只需证明面PCD内的直线CD，垂直平面PAD内的两条相交直线AD、PD即可；（2）过点B作BE∥CA，且BE=CA，∠PBE是AC与PB所成的角，解直角三角形PEB求AC与PB所成的角；（3）作AN⊥CM，垂足为N，连接BN，说明∠ANB为所求二面角的平面角，在三角形AMC中，用余弦定理求面AMC与面BMC所成二面角的大小．
【考点精析】关于本题考查的平面与平面垂直的判定和空间角的异面直线所成的角，需要了解一个平面过另一个平面的垂线，则这两个平面垂直；已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则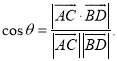才能得出正确答案．