题目内容
【题目】已知： 
、 
、 
是同一平面上的三个向量，其中 =（1，2）．
（1）若| |=2 
，且 ∥ ，求 的坐标．
（2）若| |= 
，且 +2 与2 ﹣ 垂直，求 与 的夹角θ
【答案】
（1）设 
∵ 
∥ 
且| |=2 
∴ 
，
∴x=±2
∴ =（2，4）或 =（﹣2，﹣4）
（2）∵（ +2 
）⊥（2 ﹣ ）
∴（ +2 ）（2 ﹣ ）=0
∴2 2+3 ﹣2 2=0
∴2| |2+3| || |cosθ﹣2| |2=0
∴2×5+3× × 
=0
∴cosθ=﹣1
∴θ=π+2kπ
∵θ∈[0，π]
∴θ=π
【解析】（1）设出 的坐标，利用它与 平行以及它的模等于2 ，待定系数法求出 的坐标．（2）由 +2 与2 ﹣ 垂直，数量积等于0，求出夹角θ的余弦值，再利用夹角θ的范围，求出此角的大小．
【考点精析】掌握数量积表示两个向量的夹角和数量积判断两个平面向量的垂直关系是解答本题的根本，需要知道设
、
都是非零向量，
，
，
是与
的夹角，则
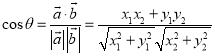；若平面
的法向量为
，平面
的法向量为
，要证
，只需证
，即证
;即：两平面垂直
两平面的法向量垂直．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
