题目内容
设圆锥曲线 的两个焦点分别为
的两个焦点分别为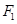 、
、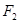 ,若曲线
,若曲线 上存在点
上存在点 满足
满足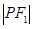 :
: :
: =4:3:2,则曲线
=4:3:2,则曲线 的离心率等于( )
的离心率等于( )
A. | B. | C. | D. |
D
解析试题分析:根据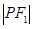 :
: :
: =4:3:2,不妨设
=4:3:2,不妨设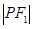 =4m,
=4m, =3m,
=3m, =2m,
=2m,
∴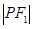 +
+ =6m>
=6m> =3m,此时曲线为椭圆,且曲线C的离心率等于
=3m,此时曲线为椭圆,且曲线C的离心率等于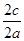 =
= ;
;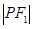 -
- =6m<
=6m< =3m,,此时曲线为双曲线,且曲线C的离心率等于
=3m,,此时曲线为双曲线,且曲线C的离心率等于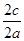 =
= ,
,
故选D。
考点:本题主要考查圆锥曲线的定义及其几何性质。
点评:简单题,确定曲线的离心率,正确判断曲线的类型是解题的关键。

练习册系列答案
相关题目
若 是任意实数,则方程x2+4y2sin
是任意实数,则方程x2+4y2sin =1所表示的曲线一定不是( )
=1所表示的曲线一定不是( )
| A.圆 | B.双曲线 | C.直线 | D.抛物线 |
若 的焦点与
的焦点与 的左焦点重合,则
的左焦点重合,则 ( )
( )
| A.-2 | B.2 | C.-4 | D.4 |
斜率为 的直线与双曲线
的直线与双曲线 (a>0,b>0)恒有两个公共点,则双曲线离心率的取值范围是
(a>0,b>0)恒有两个公共点,则双曲线离心率的取值范围是
A. | B. | C. | D. |
到两互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是( )。
| A.直线 | B.椭圆 | C.抛物线 | D.双曲线 |
如图,用与底面成 角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
A. | B. | C. | D.非上述结论 |
椭圆 和双曲线
和双曲线 的公共焦点为
的公共焦点为 ,
, 是两曲线的一个交点,那么
是两曲线的一个交点,那么 的值是( )
的值是( )
A. | B. | C. | D. |
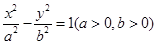 的右焦点F作与
的右焦点F作与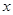 轴垂直的直线,分别与双曲线、双曲线的渐近线交于点
轴垂直的直线,分别与双曲线、双曲线的渐近线交于点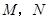 (均在第一象限内),若
(均在第一象限内),若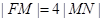 ,则双曲线的离心率为
,则双曲线的离心率为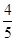
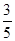
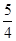
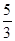
 +
+ =1(a
=1(a b
b +
+ =1(a
=1(a ,则椭圆的离心率为( )
,则椭圆的离心率为( ) B.
B. C.
C.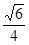 D.
D.