题目内容
如图,用与底面成 角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
A. | B. | C. | D.非上述结论 |
A
解析试题分析:∵设圆柱的底面直径为d,截面与底面成30°,∴椭圆的短轴长d,
椭圆的长轴长2a=  。
。
根据 得,椭圆的半焦距长
得,椭圆的半焦距长 =
=  d
d
则椭圆的离心率e= ,故选A.
,故选A.
考点:本题主要考查椭圆的几何性质。
点评:简单题,一般的,若与底面夹角为θ平面α截底面直径为d圆柱,则得到的截面必要椭圆,且椭圆的短轴长等于圆柱的底面直径,长轴长等于 。
。

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
椭圆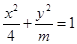 的焦距为2,则
的焦距为2,则 的值为( )
的值为( )
| A.3 | B. | C.3或5 | D.3或 |
双曲线 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则 ( )
( )
A. | B. | C. | D. |
已知直线 交于A,B两点,且
交于A,B两点,且 (其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
(其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
A. 2 2 | B. |
C. 1 1 | D.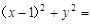 4 4 |
设定点M(3, )与抛物线
)与抛物线 =2x上的点P的距离为
=2x上的点P的距离为 ,P到抛物线准线l的距为
,P到抛物线准线l的距为 ,则
,则 +
+ 取最小值时,P点的坐标为
取最小值时,P点的坐标为
| A.(0,0) | B.(1, ) ) | C.(2,2) | D.( ,- ,- ) ) |
已知函数 与函数
与函数 ,若
,若 与
与 的交点在直线
的交点在直线 的两侧,则实数
的两侧,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
若曲线 :
: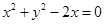 与曲线
与曲线 :
: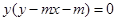 有四个不同的交点,则实数m的取值范围是( )
有四个不同的交点,则实数m的取值范围是( )
A.( , , ) ) | B.( ,0)∪(0, ,0)∪(0, ) ) |
C.[ , , ] ] | D.( , , )∪( )∪( ,+ ,+ ) ) |
在抛物线y2=2px上,横坐标为4的点到焦点的距离为5,则p的值为( )
A. | B.1 | C.4 | D.2 |
 的两个焦点分别为
的两个焦点分别为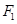 、
、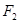 ,若曲线
,若曲线 满足
满足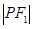 :
: :
: =4:3:2,则曲线
=4:3:2,则曲线


