题目内容
北京奥运会主体育场“鸟巢”的简化钢结构俯视图如图所示,内外两圈的钢骨架是离心率相同的椭圆,从外层椭圆顶点A、B向内层椭圆引切线AC、BD设内层椭圆方程为 +
+ =1(a
=1(a b
b 0),外层椭圆方程为
0),外层椭圆方程为 +
+ =1(a
=1(a b
b 0,m
0,m 1),AC与BD的斜率之积为-
1),AC与BD的斜率之积为- ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A. B.
B. C.
C.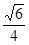 D.
D.
A
解析试题分析:解:易知A(ma,0),设切线AC的方程为y=k1 (x-ma),则联立方程 ,得(b2 +a2
,得(b2 +a2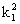 )x2 -2ma3
)x2 -2ma3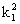 x+m2 a4
x+m2 a4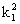 -a2 b2 =0,由△=0得
-a2 b2 =0,由△=0得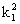 =
= ·
· ,同理,设切线BD的方程为y=k2 x+mb.可求得
,同理,设切线BD的方程为y=k2 x+mb.可求得 =
= ·(m2一1),
·(m2一1),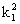
 =(kl k2 )2 =
=(kl k2 )2 = ,又kl k2 =一
,又kl k2 =一 ,所以
,所以 =
= ,e2 =
,e2 = =1一
=1一 =
= ,e=
,e= ,故选A
,故选A
考点:椭圆的性质
点评:解决的关键是利用联立方程组,结合判别式,以及切线方程来得到求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知焦点在 轴上的椭圆
轴上的椭圆 的离心率是
的离心率是 ,则
,则 的值为 ( )
的值为 ( )
A.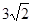 | B. | C. | D. |
抛物线x2=-y,的准线方程是( )。
A. | B. | C. | D. |
双曲线 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则 ( )
( )
A. | B. | C. | D. |
设定点M(3, )与抛物线
)与抛物线 =2x上的点P的距离为
=2x上的点P的距离为 ,P到抛物线准线l的距为
,P到抛物线准线l的距为 ,则
,则 +
+ 取最小值时,P点的坐标为
取最小值时,P点的坐标为
| A.(0,0) | B.(1, ) ) | C.(2,2) | D.( ,- ,- ) ) |
设 是椭圆
是椭圆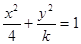 的离心率,且
的离心率,且 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
| A. (0,3) | B. (3, ) ) |
C. (0,3) ( (  ,+ ,+ ) ) | D. (0,2) |
 :抛物线
:抛物线 的准线方程为
的准线方程为 ;命题
;命题 :平面内两条直线的斜率相等是两条直线平行的充分不必要条件;则下列命题是真命题的是( )
:平面内两条直线的斜率相等是两条直线平行的充分不必要条件;则下列命题是真命题的是( )



 ,
, 分别是双曲线
分别是双曲线 (
(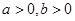 )的左右焦点,P为双曲线右支上一点,且满足
)的左右焦点,P为双曲线右支上一点,且满足 ,若直线
,若直线 与圆
与圆 相切,则双曲线的离心率e的值为
相切,则双曲线的离心率e的值为
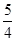

 的两个焦点分别为
的两个焦点分别为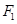 、
、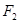 ,若曲线
,若曲线 满足
满足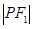 :
: :
: =4:3:2,则曲线
=4:3:2,则曲线


