题目内容
到两互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是( )。
| A.直线 | B.椭圆 | C.抛物线 | D.双曲线 |
D
解析试题分析:先做出两条异面直线的公垂线,以其中一条直线为x轴,公垂线与x轴交点为原点,公垂线所在直线为z轴,过x且垂直于公垂线的平面为xoy平面,建立空间直角坐标系,则两条异面直线的方程可得,设空间内任意点设它的坐标是(x,y,z)根据它到两条异面直线的距离相等,求得z的表达式,把z=0和z=a代入即可求得x和y的关系,根据其方程判断轨迹.先做出两条一面直线的公垂线,以其中一条直线为x轴,公垂线与x轴交点为原点,公垂线所在直线为z轴,过x且垂直于公垂线的平面为xoy平面,建立空间直角坐标系,则两条异面直线的方程就分别是y=0,z="0" 和x=0,z=a(a是两异面直线公垂线长度,是个常数)空间内任意点设它的坐标是(x,y,z)那么由已知,它到两条异面直线的距离相等,即 ,过一条直线且平行于另一条直线的平面是z=0和z=a,分别代入所得式子z=0时代入可以得到y2-x2=-a2,图形是个双曲线z=a时,代入可以得到y2-x2=a2,图形也是个双曲线,故选D
,过一条直线且平行于另一条直线的平面是z=0和z=a,分别代入所得式子z=0时代入可以得到y2-x2=-a2,图形是个双曲线z=a时,代入可以得到y2-x2=a2,图形也是个双曲线,故选D
考点:双曲线方程
点评:本题主要考查了双曲线的方程.考查了学生分析归纳和推理的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
经过点 ,并且对称轴都在坐标轴上的等轴双曲线的方程为( )
,并且对称轴都在坐标轴上的等轴双曲线的方程为( )
A. | B. |
C. 或 或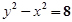 | D. |
直线 与曲线
与曲线 相切于点
相切于点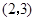 ,则
,则 的值为 ( )
的值为 ( )
| A.5 | B. 6 | C. 4 | D. 9 |
方程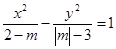 表示双曲线,则
表示双曲线,则 的取值范围是
的取值范围是
A. | B. 或 或 或 或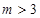 |
C. 或 或 | D. 或 或 |
双曲线 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则 ( )
( )
A. | B. | C. | D. |
已知直线 交于A,B两点,且
交于A,B两点,且 (其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
(其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
A. 2 2 | B. |
C. 1 1 | D.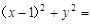 4 4 |
已知函数 与函数
与函数 ,若
,若 与
与 的交点在直线
的交点在直线 的两侧,则实数
的两侧,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
 的两个焦点分别为
的两个焦点分别为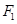 、
、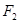 ,若曲线
,若曲线 满足
满足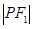 :
: :
: =4:3:2,则曲线
=4:3:2,则曲线



 在抛物线
在抛物线 上,那么点
上,那么点 (2,-1)的距离与点
(2,-1)的距离与点


