题目内容
若曲线y=x2+ax+b在点(0,b)处的切线方程是x﹣y+1=0,则( )
| A.a=1,b=1 | B.a=﹣1,b=1 |
| C.a=1,b=﹣1 | D.a=﹣1,b=﹣1 |
A
∵y'=2x+a|x=0=a,
∵曲线y=x2+ax+b在点(0,b)处的切线方程x﹣y+1=0的斜率为1,
∴a=1,
又切点在切线x﹣y+1=0,
∴0﹣b+1=0
∴b=1.
故选:A
∵曲线y=x2+ax+b在点(0,b)处的切线方程x﹣y+1=0的斜率为1,
∴a=1,
又切点在切线x﹣y+1=0,
∴0﹣b+1=0
∴b=1.
故选:A

练习册系列答案
相关题目
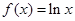 ,
,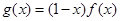
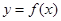 在点(1,0)处的切线方程;
在点(1,0)处的切线方程; 及
及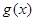 在区间
在区间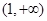 上的单调性;
上的单调性; 在
在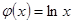
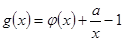 在点
在点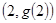 处的切线与直线
处的切线与直线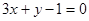 平行,求
平行,求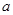 的值;
的值;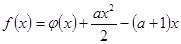 ,
, ,且
,且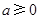 .求函数
.求函数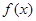 的单调递增区间.
的单调递增区间.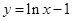 在
在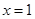 处的切线方程为 .
处的切线方程为 .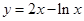 在点
在点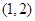 处的切线方程是 .
处的切线方程是 .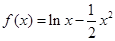 在
在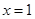 处的切线方程为 .
处的切线方程为 .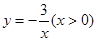 上,且与直线
上,且与直线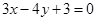 相切的面积最小的圆的方程是 .
相切的面积最小的圆的方程是 .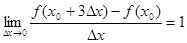 ,则
,则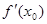 = .
= . 在
在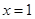 处的导数为1,则
处的导数为1,则 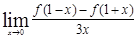 =
=