题目内容
【题目】已知函数f（x）=2cosxsin（x﹣ 
）+ 
．
（1）求函数f（x）的对称轴方程；
（2）若方程sin2x+2|f（x+ 
）|﹣m+1=0在x∈[﹣ 
， 
]上有三个实数解，求实数m的取值范围．
【答案】
（1）解：f（x）=2cosxsin（x﹣ 
）+ 
= 
sinxcosx﹣ 
= 
=sin（2x﹣ ），
∴函数f（x）的对称轴方程x= 
，k∈Z
（2）解：方程sin2x+2|f（x+ 
）|﹣m+1=0可化为方程sin2x+2|sin2x|=m﹣1．
令g（x）=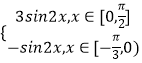 
若方程有三个实数解，则m﹣1=1或0＜m﹣1＜ 
∴m=2或1＜m＜1+
【解析】（1）利用差角的正弦公式、二倍角公式、辅助角公式，化简函数，即可求函数f（x）的对称轴方程；（2）方程sin2x+2|f（x+ ）|﹣m+1=0可化为方程sin2x+2|sin2x|=m﹣1．令g（x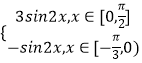）= ，根据方程有三个实数解，则m﹣1=1或0＜m﹣1＜ ，即可求实数m的取值范围．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
