题目内容
【题目】设直线l：y＝2x＋2，若l与椭圆
的交点为A，B，点P为椭圆上的动点，则使△PAB的面积为
的点P的个数为( )
A. 0 B. 1 C. 2 D. 3
【答案】D
【解析】
由直线l的方程与椭圆x2+
=1的方程组成方程组，求出弦长AB，计算AB边上的高h，
设出P的坐标，由点P到直线y=2x+2的距离d=h，结合椭圆的方程，求出点P的个数来．
由直线l的方程与椭圆x2+=1的方程组成方程组
，
解得
或
，
则A（0，2），B（﹣1，0），
∴AB=
=
，
∵△PAB的面积为
﹣1，
∴AB边上的高为h=
=
．
设P的坐标为（a，b），代入椭圆方程得：a2+
=1，
P到直线y=2x+2的距离d=
=，
即2a﹣b=2﹣4或2a﹣b=﹣2；
联立得：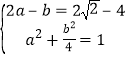
①或
②，
①中的b消去得：2a2﹣2（﹣2）a+5﹣4=0，
∵△=4（﹣2）2﹣4×2×（5﹣4）＞0，∴a有两个不相等的根，∴满足题意的P的坐标有2个；
由②消去b得：2a2+2a+1=0，
∵△=（2）2﹣4×2×1=0，∴a有两个相等的根，满足题意的P的坐标有1个．
综上，使△PAB面积为﹣1的点P的个数为3．
故选：D．
练习册系列答案
相关题目
