题目内容
【题目】如图，已知等边△ABC中，E，F分别为AB，AC边的中点，N为BC边上一点，且CN= 
BC，将△AEF沿EF折到△A′EF的位置，使平面A′EF⊥平面EF﹣CB，M为EF中点． 
（1）求证：平面A′MN⊥平面A′BF；
（2）求二面角E﹣A′F﹣B的余弦值．
【答案】
（1）证明：如图所示，取BC的中点G，连接MG，则MG⊥EF，
∵平面A′EF⊥平面EFCB，平面A′EF∩平面EFCB=EF，
∴MG⊥平面A′EF，∴MG⊥A′M，又A′M⊥EF，
因此可以建立空间直角坐标系．不妨设BC=4．
M（0，0，0），A′（0，0， 
），N（﹣1， ，0），
B（2， ，0），F（﹣1，0，0）．
=（0，0， ）， 
=（﹣1， ，0），
=（1，0， ）， 
=（3， ，0）．
设平面A′MN的法向量为 
=（x，y，z），
则 
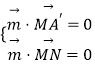，即 
，
取 = 
．
同理可得平面A′BF的法向量 
= 
．
∵ 
=3﹣3+0=0，∴ 
，
∴平面A′MN⊥平面A′BF
（2）解：由（1）可得平面A′BF的法向量 = ．
取平面EA′F的法向量 
=（0，1，0）．
则cos 
= 
= 
=- 
，
由图可知：二面角E﹣A′F﹣B的平面角为锐角，
∴二面角E﹣A′F﹣B的平面角的余弦值为 ．
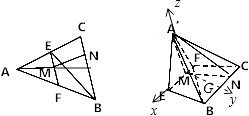
【解析】（1）如图所示，取BC的中点G，连接MG，则MG⊥EF，利用面面与线面垂直的性质与判定定理可得：MG⊥A′M，又A′M⊥EF，因此可以建立空间直角坐标系．不妨设BC=4．只要证明平面法向量的夹角为直角即可证明平面A′MN⊥平面A′BF．（2）利用两个平面的法向量的夹角即可得出．
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点，需要掌握一个平面过另一个平面的垂线，则这两个平面垂直才能正确解答此题．
