题目内容
已知椭圆
=1(a＞b＞0),点P为其上一点，F1、F2为椭圆的焦点，∠F1PF2的外角平分线为l，点F2关于l的对称点为Q，F2Q交l于点R.
(1)当P点在椭圆上运动时，求R形成的轨迹方程；
(2)设点R形成的曲线为C，直线l: y=k(x+
a)与曲线C相交于A、B两点，当△AOB的面积取得最大值时，求k的值.
=1(a＞b＞0),点P为其上一点，F1、F2为椭圆的焦点，∠F1PF2的外角平分线为l，点F2关于l的对称点为Q，F2Q交l于点R. (1)当P点在椭圆上运动时，求R形成的轨迹方程；
(2)设点R形成的曲线为C，直线l: y=k(x+
a)与曲线C相交于A、B两点，当△AOB的面积取得最大值时，求k的值.(1) R的轨迹方程为： x2+y2=a2(y≠0) (2)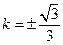
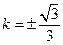
(1)∵点F2关于l的对称点为Q，连接PQ，
∴∠F2PR=∠QPR，|F2R|=|QR|，|PQ|=|PF2|
又因为l为∠F1PF2外角的平分线，故点F1、P、Q在同一直线上，设存在R(x0,y0）,Q(x1,y1),F1(－c,0),F2(c,0).
|F1Q|=|F2P|+|PQ|=|F1P|+|PF2|=2a,则(x1+c)2+y12=(2a)2.
又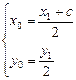
得x1=2x0－c,y1=2y0。
∴(2x0)2+(2y0)2=(2a)2，∴x02+y02=a2.
故R的轨迹方程为： x2+y2=a2(y≠0)
(2)如右图，∵S△AOB=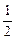
|OA|·|OB|·sinAOB=
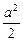sinAOB
当∠AOB=90°时，S△AOB最大值为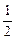a2.
此时弦心距|OC|=
.
在Rt△AOC中，∠AOC=45°，
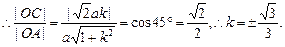
∴∠F2PR=∠QPR，|F2R|=|QR|，|PQ|=|PF2|
又因为l为∠F1PF2外角的平分线，故点F1、P、Q在同一直线上，设存在R(x0,y0）,Q(x1,y1),F1(－c,0),F2(c,0).
|F1Q|=|F2P|+|PQ|=|F1P|+|PF2|=2a,则(x1+c)2+y12=(2a)2.
又
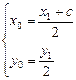
得x1=2x0－c,y1=2y0。
∴(2x0)2+(2y0)2=(2a)2，∴x02+y02=a2.
故R的轨迹方程为： x2+y2=a2(y≠0)
(2)如右图，∵S△AOB=
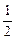|OA|·|OB|·sinAOB=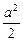sinAOB当∠AOB=90°时，S△AOB最大值为
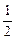a2.此时弦心距|OC|=
.在Rt△AOC中，∠AOC=45°，
练习册系列答案
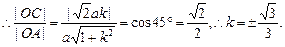
小题狂做系列答案
相关题目
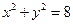上的每一点的纵坐标压缩到原来的
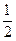,对应的横坐标不变,得到曲线C；设
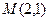，平行于OM的直线
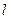在y轴上的截距为m(m≠0),直线
的方程；
：
上的一点
作一个长轴最短的椭圆，使其焦点为
，则椭圆的方程为 .
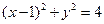与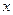
轴负半轴交于B点，过B的弦BE与
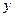轴正半轴交于D点，且2BD=DE，曲线C是以A，B为焦点且过D点的椭圆。（1）求椭圆的方程；（2）点P在椭圆C上运动，点Q在圆A上运动，求PQ+PD的最大值。
的左右焦点分别为F1,F2，若过点P（0，-2）及F1的直线交椭圆于A,B两点，求⊿ABF2的面积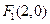
是椭圆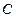
的一个焦点，相应准线为
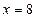，离心率为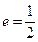
。
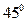的直线被曲线
的内接矩形的面积的最大值为 
过点（－2，
），则其焦距为（ ）
的离心率为
，则它的长半轴长为_______________.