题目内容
已知椭圆 的左右焦点分别为F1,F2,若过点P(0,-2)及F1的直线交椭圆于A,B两点,求⊿ABF2的面积
的左右焦点分别为F1,F2,若过点P(0,-2)及F1的直线交椭圆于A,B两点,求⊿ABF2的面积
 的左右焦点分别为F1,F2,若过点P(0,-2)及F1的直线交椭圆于A,B两点,求⊿ABF2的面积
的左右焦点分别为F1,F2,若过点P(0,-2)及F1的直线交椭圆于A,B两点,求⊿ABF2的面积由题可知:直线 方程为
方程为
由 可得
可得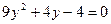 ,
,

 方程为
方程为
由
 可得
可得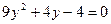 ,
,

在利用弦长公式 (k为直线斜率)或焦(左)半径公式
(k为直线斜率)或焦(左)半径公式 时,应结合韦达定理解决问题。
时,应结合韦达定理解决问题。
 (k为直线斜率)或焦(左)半径公式
(k为直线斜率)或焦(左)半径公式 时,应结合韦达定理解决问题。
时,应结合韦达定理解决问题。
练习册系列答案
相关题目
题目内容
 的左右焦点分别为F1,F2,若过点P(0,-2)及F1的直线交椭圆于A,B两点,求⊿ABF2的面积
的左右焦点分别为F1,F2,若过点P(0,-2)及F1的直线交椭圆于A,B两点,求⊿ABF2的面积 方程为
方程为
 可得
可得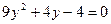 ,
,

 (k为直线斜率)或焦(左)半径公式
(k为直线斜率)或焦(左)半径公式 时,应结合韦达定理解决问题。
时,应结合韦达定理解决问题。