题目内容
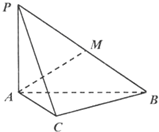
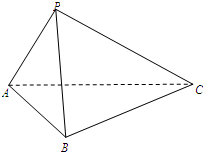
如图,在三棱锥P-ABC中,底面△ABC为等边三角形,∠APC=90°,AC=2PA=4,且平面PAC⊥平面ABC.
(1)求三棱锥P-ABC的体积;
(2)求二面角B-AP-C的余弦值;
(3)判断在线段AC上是否存在点Q,使得△PQB为直角三角形?若存在,找出所有符合要求的点Q,并求
的值;若不存在,说明理由.
(1)求三棱锥P-ABC的体积;
(2)求二面角B-AP-C的余弦值;
(3)判断在线段AC上是否存在点Q,使得△PQB为直角三角形?若存在,找出所有符合要求的点Q,并求
| AQ |
| QC |

(1)如图,过P作PO⊥AC,∵平面PAC⊥平面ABC,∴PO⊥平面ABC.
在△APC中,∠APC=90°,AC=2PA=4,∴∠PAC=60°,∴PO=APsin60°=
,AO=1.
∴三棱锥P-ABC的体积V=
PO×S△ABC=
×
×
×42=4.
(2)取AC,AB的中点分别为M,N,连接BM,ON.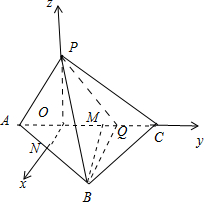
在等边△ABC中,∵O、N分别为AM、AB的中点,∴ON∥BM,∴ON⊥AC.
由(1)可知:PO⊥平面ABC,∴PO⊥ON,PO⊥OC,因此可以建立如图所示的空间直角坐标系.
A(0,-1,0),B(2
,1,0),C(0,3,0),P(0,0,
).
∴
=(2
,2,0),
=(0,1,
).
设
=(x,y,z)为平面PAB的一个法向量,则
•
=0,
•
=0.
∴
,令y=-
,则x=1,z=1.∴
=(1,-
,1).
∵x轴⊥平面APC,∴可以取
=(1,0,0)作为平面APC的法向量.
设二面角B-AP-C的大小为θ,由图可知θ∈(0,
).
∴cosθ=
=
=
.
∴二面角B-AP-C的余弦值为
.
(3)在线段AC上存在点Q,使得△PQB为直角三角形.
设Q(0,m,0)(-1≤m≤3).
则
=(0,m,-
),
=(-2
,m-1,0),
=(2
,1,-
).
①当∠PQB=90°时,则
•
=0,得m(m-1)=0,解得m=0或1.
当m=0时,Q与O重合,△PQB为直角三角形,且
=
;
当m=1时,Q与M重合,△PQB为直角三角形,且
=1;
②当∠PBQ=90°时,则
•
=0,得-12+m-1=0,解得m=13,不符合题意,应舍去;
③当∠BPQ=90°时,则
•
=0,得m+3=0=0,解得m=-3,不符合题意,应舍去.
综上可知:在线段AC上存在点Q,使得△PQB为直角三角形,且
=
或
=1.
在△APC中,∠APC=90°,AC=2PA=4,∴∠PAC=60°,∴PO=APsin60°=
| 3 |
∴三棱锥P-ABC的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| ||
| 4 |
(2)取AC,AB的中点分别为M,N,连接BM,ON.

在等边△ABC中,∵O、N分别为AM、AB的中点,∴ON∥BM,∴ON⊥AC.
由(1)可知:PO⊥平面ABC,∴PO⊥ON,PO⊥OC,因此可以建立如图所示的空间直角坐标系.
A(0,-1,0),B(2
| 3 |
| 3 |
∴
| AB |
| 3 |
| AP |
| 3 |
设
| n |
| n |
| AB |
| n |
| AP |
∴
|
| 3 |
| n |
| 3 |
∵x轴⊥平面APC,∴可以取
| m |
设二面角B-AP-C的大小为θ,由图可知θ∈(0,
| π |
| 2 |
∴cosθ=
|
| ||||
|
|
| 1 | ||||
|
| ||
| 5 |
∴二面角B-AP-C的余弦值为
| ||
| 5 |
(3)在线段AC上存在点Q,使得△PQB为直角三角形.
设Q(0,m,0)(-1≤m≤3).
则
| PQ |
| 3 |
| BQ |
| 3 |
| PB |
| 3 |
| 3 |
①当∠PQB=90°时,则
| PQ |
| BQ |
当m=0时,Q与O重合,△PQB为直角三角形,且
| AQ |
| QB |
| 1 |
| 3 |
当m=1时,Q与M重合,△PQB为直角三角形,且
| AQ |
| QB |
②当∠PBQ=90°时,则
| PB |
| BQ |
③当∠BPQ=90°时,则
| PB |
| PQ |
综上可知:在线段AC上存在点Q,使得△PQB为直角三角形,且
| AQ |
| QB |
| 1 |
| 3 |
| AQ |
| QB |

练习册系列答案
相关题目