Question

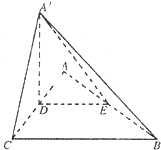
把边长为a的正△ABC沿高线AD折成60°的二面角，这时A到边BC的距离是（　　）

A． 15 4 a

B． 6 3 a

C． 13 4 a

D． 3 2 a

Answer 1

如图，因为AD是正△ABC的高线，所以∠BDC即为二面角的平面角，即∠BDC=60°，

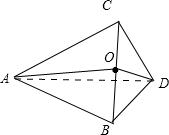
又因为△ABC是边长为a的正三角形，D是边BC的中点，
所以△BDC为正三角形，并且CD=BD=BC=

a

2

，
过D作DO垂直于BC于O，
所以O是BC的中点，连接AO．
因为AD⊥底面BDC，所以AD⊥BC，
又因为DO⊥BC，并且AD∩DO=D，
所以BC⊥面ADO，所以BC⊥AO，即AO即为点A到BC的距离．
由题意可得：正三角形ABC的边长为a，所以AD=

3

2

a，
因为在正三角形BDC中，边长为

a

2

，所以BC边上的高DO=

3

4

a，
所以在直角三角形ADO中，可得AO=

( 3 2 a)2+( 3 4 a)2

=

15

4

a．
故选A．