题目内容
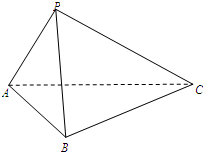
三棱锥P-ABC的两侧面PAB，PBC都是边长为2的正三角形，AC=
，则二面角A-PB-C的大小为______．
| 3 |
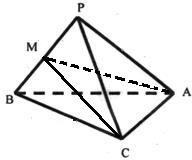
取PB的中点M，连接AM，CM．
则AM⊥PB，CM⊥PB．
故∠AMC为二面角A-PB-C的平面角．
在△AMC中可得AM=CM=
，而AC=
，则△AMC为正三角形，
∴∠AMC=60°，
∴二面角A-PB-C的大小为60°，
故答案为60°．
则AM⊥PB，CM⊥PB．
故∠AMC为二面角A-PB-C的平面角．
在△AMC中可得AM=CM=
| 3 |
| 3 |
∴∠AMC=60°，
∴二面角A-PB-C的大小为60°，
故答案为60°．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
