题目内容
(16分)如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是地面边长的 倍,
倍,
P为侧棱SD上的点。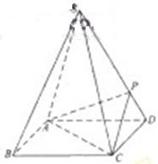
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E,使得BE∥平
面PAC。若存在,求SE:EC的值 ;若不存在,试说明理由。
;若不存在,试说明理由。
 倍,
倍,P为侧棱SD上的点。

(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E,使得BE∥平
面PAC。若存在,求SE:EC的值
 ;若不存在,试说明理由。
;若不存在,试说明理由。略
解法一:
( Ⅰ)连BD,设AC交BD于O,由题意
Ⅰ)连BD,设AC交BD于O,由题意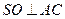 。在正方形ABCD中,
。在正方形ABCD中,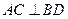 ,所以
,所以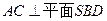 ,得
,得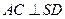 .
.
(Ⅱ)设正方形边长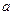 ,则
,则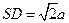 。
。
又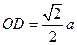 ,所以
,所以 ,
,
连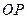 ,由(Ⅰ)知
,由(Ⅰ)知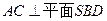 ,所以
,所以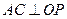 ,
,
且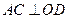 ,所以
,所以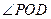 是二面角
是二面角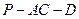 的平面角。
的平面角。
由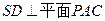 ,知
,知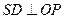 ,所以
,所以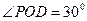 ,
,
即二面角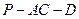 的大小为
的大小为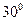 。
。
(Ⅲ)在棱SC上存在一点E,使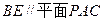
由(Ⅱ)可得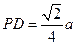 ,故可在
,故可在 上取一点
上取一点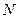 ,使
,使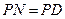 ,过
,过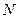 作
作 的平行线与
的平行线与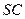 的交点即为
的交点即为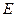 。连BN。在
。连BN。在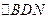 中知
中知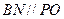 ,又由于
,又由于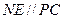 ,故平面
,故平面
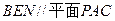 ,得
,得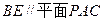 ,由于
,由于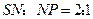 ,故
,故 .
.
解法二:
(Ⅰ);连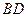 ,设
,设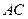 交于
交于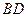 于
于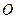 ,由题意知
,由题意知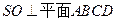 .以O为坐标原点,
.以O为坐标原点,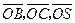 分别为
分别为 轴、
轴、 轴
轴 、
、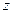 轴正方向,建立坐标系
轴正方向,建立坐标系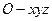 如图。
如图。
设 底面边长为
底面边长为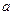 ,则高
,则高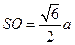 。
。
于是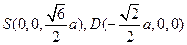
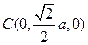


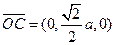
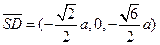
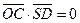
故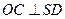
从而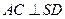
(Ⅱ)由题设知,平面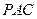 的一个法向量
的一个法向量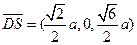 ,平面
,平面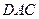 的一个法向量
的一个法向量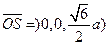 ,设所求二面角为
,设所求二面角为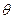 ,则
,则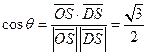 ,所求二面角的大小为
,所求二面角的大小为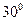
 (Ⅲ)在棱
(Ⅲ)在棱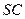 上存在一点
上存在一点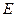 使
使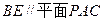 .
.
由(Ⅱ)知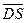 是平面
是平面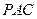 的一个法向量,
的一个法向量,
且
设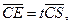

则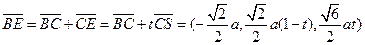
而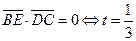
即当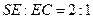 时,
时,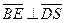


而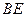 不在平面
不在平面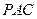 内,故
内,故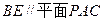
(
 Ⅰ)连BD,设AC交BD于O,由题意
Ⅰ)连BD,设AC交BD于O,由题意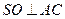 。在正方形ABCD中,
。在正方形ABCD中,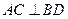 ,所以
,所以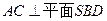 ,得
,得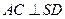 .
.(Ⅱ)设正方形边长
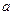 ,则
,则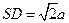 。
。又
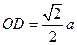 ,所以
,所以 ,
,连
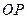 ,由(Ⅰ)知
,由(Ⅰ)知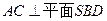 ,所以
,所以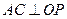 ,
, 且
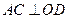 ,所以
,所以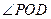 是二面角
是二面角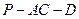 的平面角。
的平面角。由
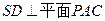 ,知
,知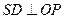 ,所以
,所以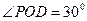 ,
,即二面角
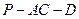 的大小为
的大小为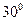 。
。(Ⅲ)在棱SC上存在一点E,使
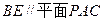
由(Ⅱ)可得
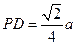 ,故可在
,故可在 上取一点
上取一点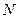 ,使
,使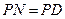 ,过
,过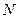 作
作 的平行线与
的平行线与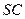 的交点即为
的交点即为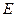 。连BN。在
。连BN。在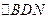 中知
中知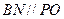 ,又由于
,又由于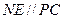 ,故平面
,故平面
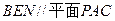 ,得
,得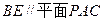 ,由于
,由于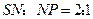 ,故
,故 .
.解法二:
(Ⅰ);连
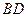 ,设
,设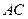 交于
交于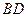 于
于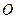 ,由题意知
,由题意知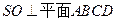 .以O为坐标原点,
.以O为坐标原点,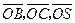 分别为
分别为 轴、
轴、 轴
轴 、
、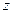 轴正方向,建立坐标系
轴正方向,建立坐标系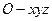 如图。
如图。设
 底面边长为
底面边长为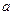 ,则高
,则高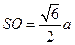 。
。于是
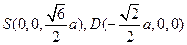
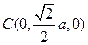


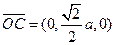
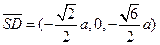
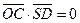
故
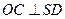
从而
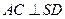
(Ⅱ)由题设知,平面
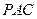 的一个法向量
的一个法向量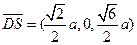 ,平面
,平面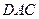 的一个法向量
的一个法向量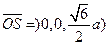 ,设所求二面角为
,设所求二面角为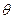 ,则
,则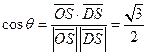 ,所求二面角的大小为
,所求二面角的大小为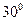
 (Ⅲ)在棱
(Ⅲ)在棱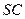 上存在一点
上存在一点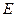 使
使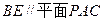 .
.由(Ⅱ)知
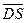 是平面
是平面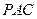 的一个法向量,
的一个法向量,且

设
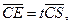

则
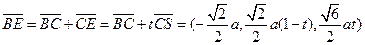
而
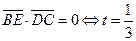
即当
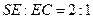 时,
时,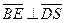


而
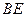 不在平面
不在平面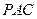 内,故
内,故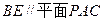

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
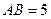 ,AA1=3,点D是AB的中点.
,AA1=3,点D是AB的中点.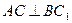
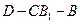 的大小.
的大小.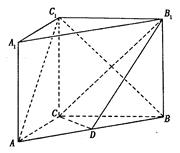

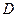 为
为 的中点,
的中点,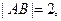
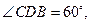
 为
为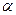 内的动点,且
内的动点,且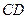 的距离为
的距离为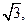 则
则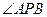 的最大值为( )
的最大值为( )
 0°
0°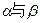 所成的二面角为80°,P为
所成的二面角为80°,P为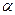 、
、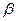 外一定点,过点P的一条直线与
外一定点,过点P的一条直线与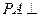 平面
平面 ,
, ,
, 为
为 的中点,则
的中点,则 与
与 的大小关系是( )
的大小关系是( )
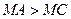


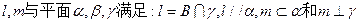 ,那么必有( )
,那么必有( )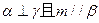

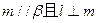
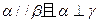
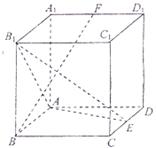
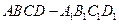 中,
中,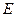 、
、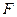 分别是
分别是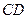 、
、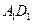 中点
中点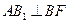 ;
;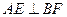 ;
;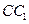 上是否存在点
上是否存在点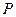 ,使
,使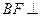 平面
平面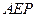 ,若存在,确 定点
,若存在,确 定点