题目内容
已知平面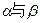 所成的二面角为80°,P为
所成的二面角为80°,P为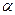 、
、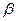 外一定点,过点P的一条直线与
外一定点,过点P的一条直线与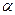 、
、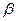 所成的角都是30°,则这样的直线有且仅有 ( )
所成的角都是30°,则这样的直线有且仅有 ( )
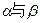 所成的二面角为80°,P为
所成的二面角为80°,P为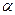 、
、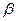 外一定点,过点P的一条直线与
外一定点,过点P的一条直线与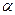 、
、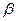 所成的角都是30°,则这样的直线有且仅有 ( )
所成的角都是30°,则这样的直线有且仅有 ( )| A.1条 | B.2条 | C.3条 | D.4条 |
D
略

练习册系列答案
相关题目
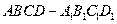 中,
中,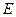 是
是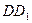 的中点,
的中点,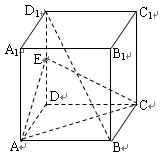
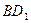 ∥平面
∥平面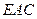 ;
; 所成角的余弦值.
所成角的余弦值. 倍,
倍,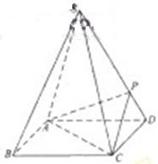
 ;若不存在,试说明理由。
;若不存在,试说明理由。 中,
中, 平面
平面 ,
,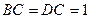 ,
,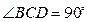 ,
,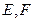 分别是
分别是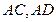 上
上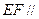 平面
平面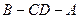 为
为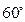 .
.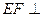 平面
平面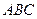 ;
; ,求直线
,求直线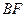 与平面
与平面 所成角的余弦值.
所成角的余弦值.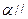 平面
平面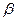 ,
,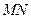 和
和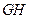 是夹在
是夹在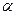 、
、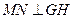 ,
,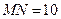 直线
直线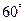 角,则线段
角,则线段 B.
B. C.
C. D.
D.
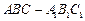 中,
中,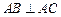 ,顶点
,顶点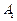 在底面
在底面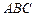 上的射影恰为点B,且
上的射影恰为点B,且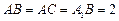 .
.
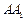 与BC所成的角的大小;
与BC所成的角的大小;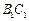 上确定一点P,使
上确定一点P,使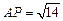 ,并求出二面角
,并求出二面角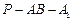 的平面角的余弦值.
的平面角的余弦值.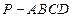 中,底面
中,底面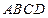 是正方形,
是正方形,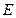 为
为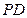 中点,若
中点,若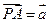 ,
,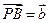 ,
,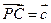 ,
, 则
则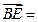 ( )
( )
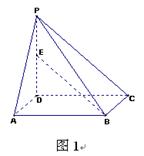

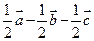
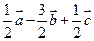
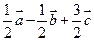
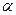 、
、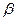 是两个不同的平面,
是两个不同的平面, 、
、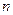 是平面
是平面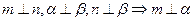 ; ②
; ②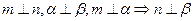 ;
;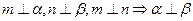 ; ④
; ④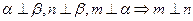 .
.