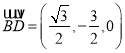题目内容
【题目】已知抛物线
的焦点为
，点
在抛物线
上，过焦点
的直线
交抛物线于
两点.
（1）求抛物线的方程以及
的值；
（2）记抛物线的准线与
轴交于点
，若
，
，求
的值.
【答案】（1）y2=4x，2（2）
【解析】
（1）依题意，
，即可求的抛物线方程，再根据抛物线的定义，直接可以写出
的值.
（2）设l：x=my+1，M（x1，y1）、N（x2，y2），联立方程，消去x，得关于y的一元二次方程，由
，得
，再根据
，求得m的值，即可求得
的值.
解：（1）
抛物线
的焦点
，
，则
，抛物线方程为
；
点
在抛物线
上
．
（2）依题意，F（1，0），设l：x=my+1，设M（x1，y1）、N（x2，y2），
联立方程
，消去x，得y2﹣4my﹣4=0．
所以
，① 且
，
又
，则（1﹣x1，﹣y1）=λ（x2﹣1，y2），即y1=﹣λy2，
代入①得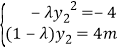
，消去y2得，
B（﹣1，0），则
，
则
（m2+1）（16m2+8）+4m4m+8=16m4+40m2+16，
当16m4+40m2+16=40，解得
，故
．
练习册系列答案
相关题目
