题目内容
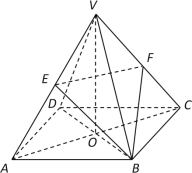
【题目】在正四棱锥![]() 中,E,F分别为棱VA,VC的中点.
中,E,F分别为棱VA,VC的中点.
(1)求证:EF∥平面ABCD;
(2)求证:平面VBD⊥平面BEF.

【答案】(1)见解析(2)见解析
【解析】
(1)由题意E,F分别为棱VA,VC的中点,得EF∥AC,利用线面平行的判定定理,即可证得EF∥平面ABCD.
(2)连结![]() ,
,![]() 交于点
交于点![]() ,连结
,连结![]() ,则
,则![]() ,进而得
,进而得![]() ,进而证得
,进而证得
EF⊥VO,EF⊥BD,由线面垂直的判定定理,得到![]() ,再由面面垂直的判定定理,即可得到平面VBD⊥平面BEF.
,再由面面垂直的判定定理,即可得到平面VBD⊥平面BEF.
(1)因为E,F分别为棱VA,VC的中点,
所以EF∥AC,
又因为![]() ,
,![]() ,
,
所以EF∥平面ABCD.
 (2)连结
(2)连结![]() ,
,![]() 交于点
交于点![]() ,连结
,连结![]() .
.
因为![]() 为正四棱锥,
为正四棱锥,
所以![]() .
.
又![]() ,所以
,所以![]() .
.
又因为![]() ,EF∥AC,
,EF∥AC,
所以EF⊥VO,EF⊥BD.
又![]() ,
,![]() ,
,
所以![]() ,
,
又![]() ,所以平面VBD⊥平面BEF.
,所以平面VBD⊥平面BEF.

练习册系列答案
相关题目
【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: .
.