题目内容
【题目】f(x)=(ax2+x﹣1)ex
(1)当a<0时,求f(x)的单调区间;
(2)若a=﹣1,f(x)的图象与g(x)= ![]() x3+
x3+ ![]() x2+m的图象有3个不同的交点,求实数m的范围.
x2+m的图象有3个不同的交点,求实数m的范围.
【答案】
(1)解:∵f'(x)=ex(ax2+x+1+2ax+1)=axex(x+ ![]() ),且a<0,
),且a<0,
∴当a∈(﹣ ![]() ,0)时,f(x)在(﹣∞,0)上是减函数,在(0,﹣
,0)时,f(x)在(﹣∞,0)上是减函数,在(0,﹣ ![]() )上是增函数,在(﹣
)上是增函数,在(﹣ ![]() ,+∞)上是减函数,
,+∞)上是减函数,
当a=﹣ ![]() 时,f(x)在(﹣∞,+∞)上单调递减;
时,f(x)在(﹣∞,+∞)上单调递减;
当a∈(﹣∞,﹣ ![]() )时,f(x)在(﹣∞,﹣
)时,f(x)在(﹣∞,﹣ ![]() )上是减函数,在(﹣
)上是减函数,在(﹣ ![]() ,0)上是增函数,在(0,+∞)上是减函数
,0)上是增函数,在(0,+∞)上是减函数
(2)解:令h(x)=f(x)﹣g(x)=(﹣x2+x﹣1)ex﹣( ![]() x3+
x3+ ![]() x2+m),
x2+m),
则h′(x)=(﹣2x+1)ex+(﹣x2+x﹣1)ex﹣(x2+x)=﹣(ex+1)(x2+x)
令h′(x)>0得﹣1<x<0,令h′(x)<0得x>0或x<﹣1.
∴h(x)在x=﹣1处取得极小值h(﹣1)=﹣ ![]() ﹣
﹣ ![]() ﹣m,在x=0处取得极大值h(0)=﹣1﹣m,
﹣m,在x=0处取得极大值h(0)=﹣1﹣m,
∵函数f(x),g(x)的图象有三个交点,即函数h(x)有3个不同的零点,
∴ ![]() 即
即 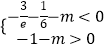 ,
,
解得:﹣ ![]() ﹣
﹣ ![]() <m<﹣1
<m<﹣1
【解析】(1)先求出函数f(x)的导函数f'(x),然后讨论a与0的大小关系,在函数的定义域内解不等式f'(x)>0和f'(x)<0,即可求出函数f(x)的单调区间;(2)令h(x)=f(x)﹣g(x),求出导数,求出单调区间,和极值,函数f(x),g(x)的图象有三个交点,即函数h(x)有3个不同的零点,即有h(﹣1)<0,且h(0)>0,解出即可.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的零点与方程根的关系的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点才能正确解答此题.
在这个区间单调递减;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点才能正确解答此题.