题目内容
【题目】已知椭圆![]() :
: ![]() (
(![]() )的右焦点在直线
)的右焦点在直线![]() :
: ![]() 上,且椭圆上任意两个关于原点对称的点与椭圆上任意一点的连线的斜率之积为
上,且椭圆上任意两个关于原点对称的点与椭圆上任意一点的连线的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 经过点
经过点![]() ,且与椭圆
,且与椭圆![]() 有两个交点
有两个交点![]() ,
, ![]() ,是否存在直线
,是否存在直线![]() :
: ![]() (其中
(其中![]() )使得
)使得![]() ,
, ![]() 到
到![]() 的距离
的距离![]() ,
, ![]() 满足
满足![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() 时符合题意.
时符合题意.
【解析】试题分析:
(1)由题意结合点差法计算可得![]() ,
, ![]() ,则椭圆的方程为
,则椭圆的方程为![]() .
.
(2)分类讨论直线的斜率存在和不存在两种情况可得:存在![]() 符合题意.
符合题意.
试题解析:
(1)设椭圆焦距为![]() (
(![]() ),右焦点 为
),右焦点 为![]() ,
,
∵直线![]() 与
与![]() 轴的交点坐标为
轴的交点坐标为![]() ∴
∴![]() .
.
设椭圆上任意一点![]() 和关于原点对称的两点
和关于原点对称的两点![]() ,
, ![]() ,
,
则有![]() ,
, ![]() ∴
∴![]()
又∵![]() 即
即![]() ∴
∴![]()
又![]() ,∴
,∴![]() ,
, ![]() .
.
∴椭圆的方程为![]() .
.
(2)存在![]() 符合题意,理由如下:
符合题意,理由如下:
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
, ![]() 联立
联立![]() ,得
,得![]()
![]() 恒成立
恒成立
![]() ,
, ![]()
不妨设![]() ,
,
∴![]()
![]()
∴![]() ,整理得
,整理得![]() ,即
,即![]() 满足条件
满足条件
当直线![]() 的斜率不存在时,显然
的斜率不存在时,显然![]() 满足条件
满足条件
综上, ![]() 时符合题意.
时符合题意.

【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱。现统计了连续5天的售出和收益情况,如下表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(Ⅰ) 若x与y成线性相关,则某天售出8箱水时,预计收益为多少元?
(Ⅱ) 期中考试以后,学校决定将诚信用水的收益,以奖学金的形式奖励给品学兼优的特困生,规定:特困生考入年级前200名,获一等奖学金500元;考入年级201—500 名,获二等奖学金300元;考入年级501名以后的特困生将不获得奖学金。甲、乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() .
.
⑴在学生甲获得奖学金条件下,求他获得一等奖学金的概率;
⑵已知甲、乙两名学生获得哪个等第的奖学金是相互独立的,求甲、乙两名学生所获得奖学金总金额X 的分布列及数学期望。
附: 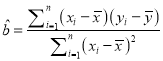 ,
, ![]() 。
。