题目内容
【题目】如图, ![]() 是边长为2的正方形
是边长为2的正方形![]() 的
的![]() 边的中点,将
边的中点,将![]() 与
与![]() 分别沿
分别沿![]() 、
、![]() 折起,使得点
折起,使得点![]() 与点
与点![]() 重合,记为点
重合,记为点![]() ,得到三棱锥
,得到三棱锥![]() .
.
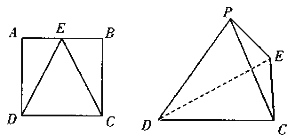
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】试题分析: (Ⅰ)由![]() ,
, ![]() ,可得
,可得![]() 平面
平面![]() ,又
,又![]() 在平面
在平面![]() 内,即可证得面面垂直;(Ⅱ)解:设点
内,即可证得面面垂直;(Ⅱ)解:设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,根据三棱锥等体积可得
,根据三棱锥等体积可得
![]() ,根据体积公式代入即可求得
,根据体积公式代入即可求得![]() .
.
试题解析:(Ⅰ)证明:∵![]() ,∴
,∴![]() ,
, ![]() .
.
∵![]() 交
交![]() 于点
于点![]() ,
, ![]() ,
, ![]() 在平面
在平面![]() 内,∴
内,∴![]() 平面
平面![]() ,
,
∵![]() 在平面
在平面![]() 内,∴平面
内,∴平面![]() 平面
平面![]() .
.
(Ⅱ)解:设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
依题意可知,三角形![]() 是底边长为2,高为2的三角形,
是底边长为2,高为2的三角形,
所以其面积为![]() .
.
由(Ⅰ)知![]() 平面
平面![]() ,易知
,易知![]() 是边长为2的等边三角形,其面积为
是边长为2的等边三角形,其面积为![]() ,
, ![]() ,
,
所以![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
点睛:本题考查面面垂直的判定以及等体积法求点线距,属于中档题目. 两平面垂直的判定有两种方法:(1)两个平面所成的二面角是直角;(2)一个平面经过另一平面的垂线.掌握基本的判定和性质定理外还应理解线线、线面、面面垂直的转化思想,逐步学会综合运用数学知识分析解决问题的能力.

练习册系列答案
相关题目