题目内容
【题目】设{an}是等差数列,数列{an}的前n项和为Sn , {bn}是各项都为正数的等比数列,且a1=b1=1,a3+b2=7,S2+b2=6 (Ⅰ)求{an},{bn}的通项公式;
(Ⅱ)求数列{anbn}的前n项和Sn .
【答案】解:(Ⅰ)设等差数列{an}的公差为d,等比数列{bn}的公比q>0,∵a1=b1=1,a3+b2=7,S2+b2=6, ∴a3﹣(1+a2)=1,∴d=2,∴an=1+2(n﹣1)=2n﹣1.b2=7﹣a3=7﹣5=2.∴q=2,bn=2n﹣1 .
(Ⅱ)anbn=(2n﹣1)2n﹣1 .
∴数列{anbn}的前n项和Sn=1+3×2+5×22+…+(2n﹣1)×2n﹣1 ,
2Sn=2+3×22+…+(2n﹣3)×2n﹣1+(2n﹣1)×2n ,
∴﹣Sn=1+2×(2+22+…+2n﹣1)﹣(2n﹣1)×2n=1+2× ![]() ﹣(2n﹣1)×2n=(3﹣2n)×2n﹣3,
﹣(2n﹣1)×2n=(3﹣2n)×2n﹣3,
∴Sn=(2n﹣3)×2n+3
【解析】(I)利用等差数列与等比数列的通项公式即可得出.(II)anbn=(2n﹣1)2n﹣1 . 利用“错位相减法”与等比数列的求和公式即可得出.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系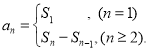 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目