题目内容
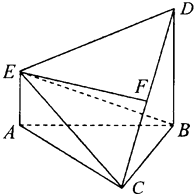
【题目】在如图的平面多边形ACBEF中,四边形ABEF是矩形,点O为AB的中点,△ABC中,AC=BC,现沿着AB将△ABC折起,直至平面ABEF⊥平面ABC,如图,此时OE⊥FC. 
(1)求证:OF⊥EC;
(2)若FC与平面ABC所成角为30°,求二面角F﹣CE﹣B的余弦值.
【答案】
(1)证明:连结OC,∵AC=BC,O是AB的中点,故OC⊥AB.
又∵平面ABC⊥平面ABEF,
故OC⊥平面ABE,
于是OC⊥OF.OC⊥OE,
又OE⊥FC,
∵OF⊥平面OFC,
∴OE⊥OF,
又∵OC⊥OF,∴OF⊥平面OEC,
∴OF⊥EC.
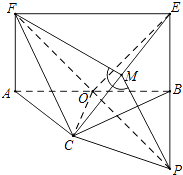
(2)由(I)得AB=2AF.不妨设AF=1,AB=2.
∵∠FCA为直线FC与平面ABC所成的角,
∴∠FCA=30°,
∴FC=EC=2,△EFC为等边三角形.
设FO∩EB=P,则O,B分别为PF,PE的中点,△PEC也是等边三角形.
取EC的中点M,连结FM,MP,则FM⊥CE,MP⊥CE,
∴∠FMP为二面角F﹣CE﹣B的平面角.
在△MFP中,FM=MP= ![]() ,FP=2
,FP=2 ![]() ,
,
故cos∠FMP= ![]() =
= ![]() =-
=- ![]() ,
,
即二面角F﹣CE﹣B的余弦值为﹣ ![]()
【解析】(Ⅰ)连结OC,则OC⊥AB,从而得到OC⊥OE,进而得到OF⊥OE,由此能证明OF⊥EC. (Ⅱ)由(I)得AB=2AF.设AF=1,AB=2.由∠FCA为直线FC与平面ABC所成的角,知∠FCA=30°,由已知条件推导出∠FMP为二面角F﹣CE﹣B的平面角,由此能求出二面角F﹣CE﹣B的余弦值
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案