题目内容
【题目】如图，在平面直角坐标系xOy中，已知以M为圆心的圆M：x2+y2﹣12x﹣14y+60=0及其上的一点A（2，4）．
（Ⅰ）是否存在直线l：y=kx+3与圆M有两个交点B，C，并且|AB|=|AC|，若有，求此直线方程，若没有，请说明理由；
（Ⅱ）设点T（t，0）满足：存在圆M上的两点P和Q，使得 
= 
，求实数t的取值范围．
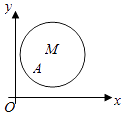
【答案】解：（Ⅰ）圆M：x2+y2﹣12x﹣14y+60=0化为（x﹣6）2+（y﹣7）2=25，圆心为M（6，7），半径为5
假设存在直线l：y=kx+3与圆M有两个交点B，C，并且|AB|=|AC|，
则AM⊥BC，∵kAM= 
，即直线l的斜率为﹣ 
则直线l：y=﹣ x+3，即4x+3y﹣9=0
圆心M（6，7）到4x+3y﹣9=0的距离d= 
即直线l与圆M无两个交点，
∴不存在直线l：y=kx+3与圆M有两个交点B，C，并且|AB|=|AC|；
（Ⅱ）设P（x1，y1），Q（x2，y2），∵A（2，4），T（t，0），
由 
= 
得， 
，由点Q在圆M上，所以（x2﹣6）2+（y2﹣7）2=25
即得（x1﹣t﹣4）2+（y1﹣3）2=25．
从而圆（x﹣6）2+（y﹣7）2=25与圆（x﹣t﹣4）2+（y﹣3）2=25上有公共点，
即5﹣5 
解得2﹣2 
≤t≤2+2 ，
∴实数t的取值范围为[2﹣2 ，2+2 ]．
【解析】（1）假设存在直线l：y=kx+3，由题意|AB|=|AC|，则AM⊥BC，即直线l的斜率为
，根据点到直线的距离即可判断出不存在这样的直线与圆有两个交点，（2）设P（x1，y1），Q（x2，y2），由向量关系表示出Q点坐标，由于点Q在圆上，可得（x1﹣t﹣4）2+（y1﹣3）2=25，若两圆有公共点，则两圆心间的距离小于半径之和，大于半径之差，即可得到实数t的取值范围.
