题目内容
18.设函数f(x)=x-$\frac{1}{x}$,对任意x∈[1,+∞),f(ax)+af(x)<0恒成立,则实数a的取值范围是( )| A. | (-∞,-1) | B. | (-1,0) | C. | (-1,1) | D. | (0,1) |
分析 根据题意和分离变量法化简f(ax)+af(x)<0,分a>0、a=0和a<0三种情况进行讨论,根据二次函数的性质和恒成立即可得出答案.
解答 解:由f(ax)+af(x)<0得,ax-$\frac{1}{ax}$+ax-$\frac{a}{x}$<0对任意x∈[1,+∞)恒成立,
所以化简得:2ax<($\frac{1}{a}+a$)$\frac{1}{x}$对任意x∈[1,+∞)恒成立,
即2ax2<$\frac{1}{a}+a$对任意x∈[1,+∞)恒成立,
①当a>0时,2x2<$\frac{1}{{a}^{2}}+1$,因为y=2x2在x∈[1,+∞)上无最大值,此时不合题意;
②当a<0时,2x2>$\frac{1}{{a}^{2}}+1$,因为y=2x2在x∈[1,+∞)上的最小值为2,
所以2>$\frac{1}{{a}^{2}}+1$,则a2>1,解得a<-1或a>1(舍去);
③当a=0时,ax=0,与f(x)定义域矛盾,不合题意;
综合可得:a<-1.
故选:A.
点评 本题考查恒成立问题的转化,分类讨论思想和分离变量法,解决恒成立问题通常转化为求函数最值,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.执行如图所示的程序框图,输出的x值为( )
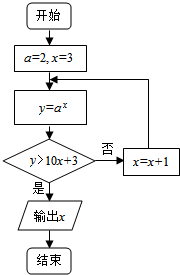

| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
13.函数y=$\frac{{\sqrt{x}}}{1-x}$的定义域是( )
| A. | [0,1)∪(1,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | [0,+∞) |
10.从含有甲乙的6名短跑运动员中任选4人参加4*100米接力,问其中甲不能跑第一棒,且乙不能跑第四棒的概率是( )
| A. | $\frac{7}{40}$ | B. | $\frac{7}{30}$ | C. | $\frac{7}{20}$ | D. | $\frac{7}{10}$ |
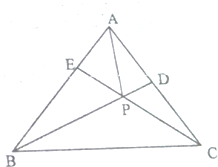 如图,在△ABC中,点D为边AC的中点,3AE=AB,BD=CE交于点P,设$\overrightarrow{a}$=$\overrightarrow{AB}$,$\overrightarrow{b}$=$\overrightarrow{AC}$
如图,在△ABC中,点D为边AC的中点,3AE=AB,BD=CE交于点P,设$\overrightarrow{a}$=$\overrightarrow{AB}$,$\overrightarrow{b}$=$\overrightarrow{AC}$