题目内容
已知数列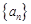 的前
的前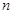 项和
项和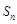 满足
满足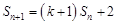 ,又
,又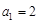 ,
,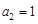 .
.
(1)求实数k的值;
(2)求证:数列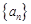 是等比数列.
是等比数列.
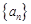 的前
的前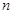 项和
项和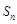 满足
满足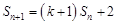 ,又
,又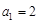 ,
,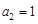 .
.(1)求实数k的值;
(2)求证:数列
 是等比数列.
是等比数列.(1)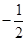 ;(2)详见解析
;(2)详见解析
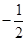 ;(2)详见解析
;(2)详见解析试题分析:(1)由
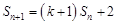 可得
可得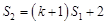 ,因为
,因为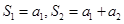 ,将
,将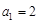 ,
,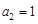 代入即可求入实数k。(2)由公式
代入即可求入实数k。(2)由公式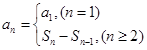 将
将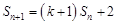 转化为
转化为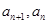 的关系,最后用等比数列的定义证明。
的关系,最后用等比数列的定义证明。试题解析:解答:(1)∵
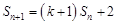 ,∴
,∴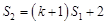 ,
,∴
 . 3分
. 3分又∵
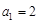 ,
,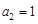 ,∴
,∴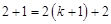 ,∴
,∴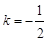 . 6分
. 6分(2)证明:由(1)知
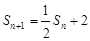 ①
①当
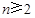 时,
时,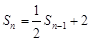 ②
②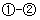 得
得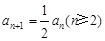 . 9分
. 9分又∵
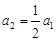 ,且
,且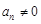
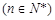 ,
,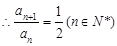 ,
,∴数列
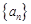 是公比为
是公比为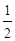 的等比数列. 12分
的等比数列. 12分 ;2等比数列的定义。
;2等比数列的定义。
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
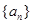 为等比数列,
为等比数列,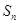 为其前
为其前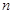 项和,已知
项和,已知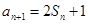 .
.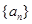 的通项公式;
的通项公式;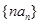 的前
的前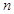 项和
项和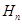 .
.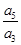
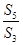


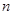 为正整数,由数列
为正整数,由数列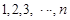 分别求相邻两项的和,得到一个有
分别求相邻两项的和,得到一个有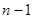 项的新数列;1+2,2+3,3+4,
项的新数列;1+2,2+3,3+4,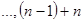 即3,5,7,
即3,5,7,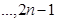 . 对这个新数列继续上述操作,这样得到一系列数列,最后一个数列只有一项.⑴记原数列为第一个数列,则第三个数列的第2项是______⑵最后一个数列的项是___________.
. 对这个新数列继续上述操作,这样得到一系列数列,最后一个数列只有一项.⑴记原数列为第一个数列,则第三个数列的第2项是______⑵最后一个数列的项是___________.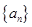 共有奇数项,所有奇数项和
共有奇数项,所有奇数项和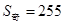 ,所有偶数项和
,所有偶数项和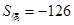 ,末项是
,末项是 ,则首项
,则首项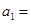 ( )
( )
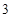
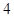
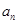 }中,若
}中,若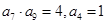 ,则
,则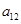 的值是 .
的值是 .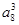 a15=243,则
a15=243,则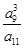 的值为( ).
的值为( ).