题目内容
17.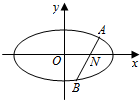 如图,设过点N(1,0)的动直线l交椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,且|AB|的最大值为4,椭圆C的离心率e=$\frac{\sqrt{3}}{2}$.
如图,设过点N(1,0)的动直线l交椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,且|AB|的最大值为4,椭圆C的离心率e=$\frac{\sqrt{3}}{2}$.(1)求椭圆C的方程;
(2)是否存在实数t,使得$\frac{1}{|NA{|}^{2}}$+$\frac{1}{|NB{|}^{2}}$+$\frac{t}{|NA|•|NB|}$为常数?求实数t的值及该常数;若不存在,请说明理由.
分析 (1)由椭圆的性质和离心率公式,可得a=2,b=1,进而得到椭圆方程;
(2)假设存在实数t,使得$\frac{1}{|NA{|}^{2}}$+$\frac{1}{|NB{|}^{2}}$+$\frac{t}{|NA|•|NB|}$为常数.设直线l的参数方程为$\left\{\begin{array}{l}{x=1+mcosα}\\{y=msinα}\end{array}\right.$(m为参数),代入椭圆方程,运用韦达定理和同角的平方关系,即可得到t和常数.
解答 解:(1)由题意可知,当AB为长轴时,
|AB|取得最大值,且为2a,
即有2a=4,∴a=2,
又e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,∴c=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$.
则b2=a2-c2=22-($\sqrt{3}$)2=1.
∴椭圆C的方程为 $\frac{{x}^{2}}{4}$+y2=1;
(2)设直线l的参数方程为$\left\{\begin{array}{l}{x=1+mcosα}\\{y=msinα}\end{array}\right.$(m为参数),
代入椭圆方程可得,(cos2α+4sin2α)m2+2mcosα-3=0,
由于(1,0)在椭圆内,判别式显然大于0,
m1+m2=-$\frac{2cosα}{co{s}^{2}α+4si{n}^{2}α}$,m1m2=-$\frac{3}{co{s}^{2}α+4si{n}^{2}α}$,
不妨设|NA|=|m1|,|NB|=|m2|,
假设存在实数t,使得$\frac{1}{|NA{|}^{2}}$+$\frac{1}{|NB{|}^{2}}$+$\frac{t}{|NA|•|NB|}$为常数.
即有$\frac{1}{{{m}_{1}}^{2}}$+$\frac{1}{{{m}_{2}}^{2}}$+t•$\frac{1}{|{m}_{1}{m}_{2}|}$=$\frac{({m}_{1}+{m}_{2})^{2}-2{m}_{1}{m}_{2}}{{(m}_{1}{m}_{2})^{2}}$+t•$\frac{1}{|{m}_{1}{m}_{2}|}$=
$\frac{4co{s}^{2}α+6co{s}^{2}α+24si{n}^{2}α}{9}$+$\frac{tco{s}^{2}α+4tsi{n}^{2}α}{3}$=$\frac{(10+3t)co{s}^{2}α+(24+12t)si{n}^{2}α}{9}$,
由10+3t=24+12t,解得t=-$\frac{14}{9}$,
即有$\frac{1}{|NA{|}^{2}}$+$\frac{1}{|NB{|}^{2}}$+$\frac{t}{|NA|•|NB|}$=$\frac{16}{3}$×$\frac{1}{9}$=$\frac{16}{27}$.
故存在实数t=-$\frac{14}{9}$,使得$\frac{1}{|NA{|}^{2}}$+$\frac{1}{|NB{|}^{2}}$+$\frac{t}{|NA|•|NB|}$为常数$\frac{16}{27}$.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,同时考查直线的参数方程的运用,代入椭圆方程,运用韦达定理,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$一l |
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
 已知椭圆C的中心在原点,左焦点为F1(-1,0),右准线方程为:x=4
已知椭圆C的中心在原点,左焦点为F1(-1,0),右准线方程为:x=4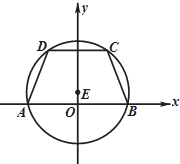 如图所示,等腰梯形ABCD的底边AB在x轴上,顶点A与顶点B关于原点O对称,且底边AB和CD的长分别为6和2$\sqrt{6}$,高为3.
如图所示,等腰梯形ABCD的底边AB在x轴上,顶点A与顶点B关于原点O对称,且底边AB和CD的长分别为6和2$\sqrt{6}$,高为3.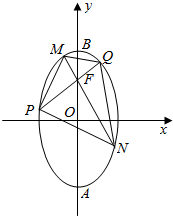 如图所示,椭圆长轴端点为点A、B、O为椭圆的中心,F为椭圆的上焦点,且$\overrightarrow{AF}•\overrightarrow{FB}=1,|\overrightarrow{OF}|=1$.
如图所示,椭圆长轴端点为点A、B、O为椭圆的中心,F为椭圆的上焦点,且$\overrightarrow{AF}•\overrightarrow{FB}=1,|\overrightarrow{OF}|=1$.