题目内容
12．已知点N（4，0），点M（x0，y0）在圆x2+y2=4上运动，点P（x，y）为线段MN的中点．（Ⅰ）求点P（x，y）的轨迹方程；
（Ⅱ）求点P到直线3x+4y-56=0的距离的最大值和最小值．
分析 （Ⅰ）用x和y表示出M的坐标代入圆的方程即可求得P的轨迹方程．
（Ⅱ）利用点到直线的距离求得圆心到直线的距离，进而利用圆心到直线的距离加或减半径即可求得最大和最小值．
解答 解：（Ⅰ）∵点P（x，y）是MN的中点，
∴$\left\{\begin{array}{l}x=\frac{{{x_0}+4}}{2}\\ y=\frac{y_0}{2}\end{array}\right.$故$\left\{\begin{array}{l}{x_0}=2x-4\\{y_0}=2y\end{array}\right.$，
将用x，y表示的x0，y0代入到${x_0}^2+{y_0}^2=4$
中得（x-2）2+y2=1．
此式即为所求轨迹方程．
（Ⅱ）由（Ⅰ）知点P的轨迹是以Q（2，0）为圆心，以1为半径的圆．
点Q到直线3x+4y-56=0的距离$d=\frac{{|{6-56}|}}{{\sqrt{{3^2}+{4^2}}}}=10$．
故点P到直线3x+4y-56=0的距离的最大值为10+1=11，最小值为10-1=9．
点评 本题主要考查了直线与圆的方程的应用．解决直线与圆的方程问题，一般是看圆心到直线的距离，利用数形结合的思想来解决．
练习册系列答案
相关题目
7．已知椭圆的长轴长是短轴长的2倍，则椭圆的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
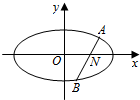如图，设过点N（1，0）的动直线l交椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）于A，B两点，且|AB|的最大值为4，椭圆C的离心率e=$\frac{\sqrt{3}}{2}$．