题目内容
7. 已知椭圆C的中心在原点,左焦点为F1(-1,0),右准线方程为:x=4
已知椭圆C的中心在原点,左焦点为F1(-1,0),右准线方程为:x=4(1)求椭圆C的标准方程;
(2)若椭圆C上点N到定点M(m,0)(0<m<2)的距离的最小值为1,求m的值及点N的坐标;
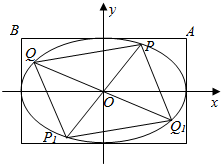
(3)分别过椭圆C的四个顶点作坐标轴的垂线,围成如图所示的矩形,A、B是所围成的矩形在x轴上方的两个顶点.若P、Q是椭圆C上两个动点,直线OP、OQ与椭圆的另一交点分别为P1、Q1,且直线OP、OQ的斜率之积等于直线OA、OB的斜率之积,试探求四边形PQP1Q1的面积是否为定值,并说明理由.
分析 (1)通过$\left\{{\begin{array}{l}{c=1}\\{\frac{a^2}{c}=4}\end{array}}\right.$,计算即得结论;
(2)设N(x,y),可得MN2的表达式是一个关于x的二次函数,分对称轴x=4m在(0,2]、(2,+∞)两种情况讨论即可;
(3)设P(x1,y1),Q(x2,y2),通过斜率计算可得${x_1}^2+{x_2}^2=4$,分x1=x2、x1≠x2两种情况讨论,利用点到直线的距离公式、三角形面积公式计算即得结论.
解答 解:(1)设椭圆的方程为:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),
由题意得:$\left\{{\begin{array}{l}{c=1}\\{\frac{a^2}{c}=4}\end{array}}$,解得:$\left\{{\begin{array}{l}{a=2}\\{c=1}\end{array}}$,
∴b2=3,
∴椭圆C的标准方程:$\frac{x^2}{4}+\frac{y^2}{3}$=1;
(2)设N(x,y),则$M{N^2}={(x-m)^2}+{y^2}={(x-m)^2}+3(1-\frac{x^2}{4})=\frac{1}{4}{x^2}-2mx+{m^2}$+3,
对称轴:x=4m,-2≤x≤2,
①当0<4m≤2,即0<m≤$\frac{1}{2}$,x=4m时,MN2min=-3m2+3=1,
解得:m2=$\frac{2}{3}>\frac{1}{4}$,不符合题意,舍去;
②当4m>2,即$\frac{1}{2}$<m<2,x=2时,MN2min=m2-4m+4=1,
解得:m=1或m=3;
∵$\frac{1}{2}$<m<2,∴m=1;
综上:m=1,N(2,0);
(3)结论:四边形PQP1Q1的面积为定值4$\sqrt{3}$.
理由如下:
由题意得:四条垂线的方程为:x=±2,y=±$\sqrt{3}$,
则$A(2,\sqrt{3})$,$B(-2,\sqrt{3})$,∴kOA•kOB=-$\frac{3}{4}$.
设P(x1,y1),Q(x2,y2),则$\frac{{{y_1}{y_2}}}{{{x_1}{x_2}}}=-\frac{3}{4}$ (*)
PQ=$\sqrt{{{({x_1}-{x_2})}^2}+{{({y_1}-{y_2})}^2}}$.
∵点P、Q在椭圆C上,∴${y_1}^2=3(1-\frac{{{x_1}^2}}{4})$,${y_2}^2=3(1-\frac{{{x_2}^2}}{4})$,
将(*)式平方得:9x12x22=16y12y22=9(4-x12)(4-x22),即x12+x22=4,
①若x1=x2,则P、P1、Q、Q2分别是直线OA、OB与椭圆的交点,
∴四个点的坐标为:$(\sqrt{2},\frac{{\sqrt{6}}}{2})$,$(\sqrt{2},-\frac{{\sqrt{6}}}{2})$,$(-\sqrt{2},\frac{{\sqrt{6}}}{2})$,$(-\sqrt{2},-\frac{{\sqrt{6}}}{2})$,
∴四边形PQP1Q1的面积为4$\sqrt{3}$;
②若x1≠x2,则直线PQ的方程可设为:y-y1=$\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}(x-{x_1})$,
化简得:(y2-y1)x-(x2-x1)y+x2y1-x1y2=0,
∴点O到直线PQ的距离为d=$\frac{{|{x_1}{y_2}-{x_2}{y_1}|}}{{\sqrt{{{({x_2}-{x_1})}^2}+{{({y_2}-{y_1})}^2}}}}$,
∴△OPQ的面积S=$\frac{1}{2}PQ•d=\frac{1}{2}|{x_1}{y_2}-{x_2}{y_1}|=\frac{1}{2}\sqrt{{x_1}^2{y_2}^2-2{x_1}{x_2}{y_1}{y_2}+{x_2}^2{y_1}^2}$
=$\frac{1}{2}\sqrt{3{x_1}^2(1-\frac{{{x_2}^2}}{4})+\frac{3}{2}{x_1}^2{x_2}^2+3{x_2}^2(1-\frac{{{x_1}^2}}{4}})=\frac{1}{2}\sqrt{3({x_1}^2+{x_2}^2)}=\frac{1}{2}\sqrt{3×4}=\sqrt{3}$.
根据椭圆的对称性,故四边形PQP1Q1的面积为4S,即为定值4$\sqrt{3}$.
综上:四边形PQP1Q1的面积为定值4$\sqrt{3}$.
点评 本题是一道直线与圆锥曲线的综合题,考查椭圆的标准方程、点的坐标、点到直线的距离、三角形面积公式,韦达定理等基础知识,考查分类讨论的思想,考查运算求解能力,注意解题方法的积累,属于难题.

| A. | $\sqrt{2}$x±y=0 | B. | x±2y=0 | C. | x±$\sqrt{2}$y=0 | D. | 2x±y=0 |
| A. | 必在圆x2+y2=2上 | B. | 必在圆x2+y2=2外 | ||
| C. | 必在圆x2+y2=2内 | D. | 以上三种情形都有可能 |
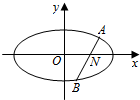 如图,设过点N(1,0)的动直线l交椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,且|AB|的最大值为4,椭圆C的离心率e=$\frac{\sqrt{3}}{2}$.
如图,设过点N(1,0)的动直线l交椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,且|AB|的最大值为4,椭圆C的离心率e=$\frac{\sqrt{3}}{2}$.