题目内容
【题目】某车间租赁甲、乙两种设备生产A，B两类产品，甲种设备每天能生产A类产品8件和B类产品15件，乙种设备每天能生产A类产品10件和B类产品25件，已知设备甲每天的租赁费300元，设备乙每天的租赁费400元，现车间至少要生产A类产品100件，B类产品200件，所需租赁费最少为__元
【答案】3800
【解析】
设甲种设备需要生产
天，乙种设备需要生产
天，根据两种产品生产件数的限制列出约束条件，根据两种设备的租赁费求出目标函数，然后利用线性规划，求出最优解即可．
设甲种设备需要生产天，乙种设备需要生产天，
该公司所需租赁费为
元，则
，
分
甲、乙两种设备生产A，B两类产品的情况为：
，做出不等式表示的平面区域，
由
解得
当经过的交点时，
目标函数取得最低为3800元．
故答案为
.
【题目】在全社会推行素质教育的大前提下，更强调了学生的全面发展，只有全面重视体育锻炼，才能使学生德智体美全面发展。为了解某高校大学生的体育锻炼情况，做了如下调查统计。该校共有学生10000人，其中男生6000人，女生4000人。为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集200位学生每周平均体育运动时间的样本数据（单位：小时）.
（1）应收集多少位女生的样本数据？
（2）根据这200个样本数据，得到学生每周平均体育运动时间的频率分布直方图，其中样本数据的分组区间为：
，
，
，
，
，
，估计该校学生每周平均体育运动时间超过4个小时的概率.
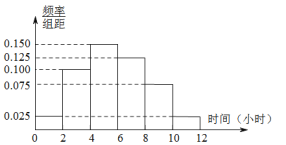
（3）在样本数据中，有50位女生的每周平均体育运动时间超过4个小时，请完成每周平均体育运动时间与性别的列联表，并判断能否在犯错误的概率不超过0.01的前提下认为“该校学生的每周平均体育运动时间与性别有关”.
女生 | 男生 | 总计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
总计 |
附：
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
