题目内容
4.已知m=${∫}_{0}^{π}$(sint+cost)dt,则${(x-\frac{1}{mx})^{3m}}$的展开式的常数项为-$\frac{5}{2}$.分析 根据题意,由定积分公式可得m=2,由二项式定理可得其展开式的通项,令x的指数为0,可得r的值,将r的值代入通项,计算可得其展开式中常数项,即可得答案
解答 解:m=${∫}_{0}^{π}$(sint+cost)dt=(-cost+sint)|${\;}_{0}^{π}$=-cosπ+sinπ-(-cos0+sin0)=1+1=2,
则${(x-\frac{1}{mx})^{3m}}$=(x-$\frac{1}{2x}$)6,
其展开式的通项为Tr+1=C6rx6-r•(-$\frac{1}{2x}$)r=C6r(-$\frac{1}{2}$)rx6-2r,
令6-2r=0,可得r=3,
此时T4=C63(-$\frac{1}{2}$)3=-$\frac{5}{2}$,
故答案为:-$\frac{5}{2}$
点评 本题考查二项式定理的运用,关键是由定积分公式求出a的值,属于中档题.

练习册系列答案
相关题目
19.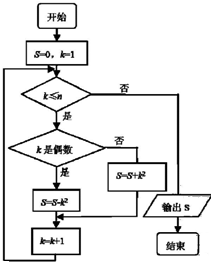 阅读如图所示的程序框图,运行相应的程序,若输入n的值为100,则输出S的值为( )
阅读如图所示的程序框图,运行相应的程序,若输入n的值为100,则输出S的值为( )
 阅读如图所示的程序框图,运行相应的程序,若输入n的值为100,则输出S的值为( )
阅读如图所示的程序框图,运行相应的程序,若输入n的值为100,则输出S的值为( )| A. | -1050 | B. | 5050 | C. | -5050 | D. | -4950 |
16.已知F1是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,过F1且垂直于x轴的直线与双曲线交于A、B两点,E是双曲线的右顶点,若△ABE是钝角三角形,则该双曲线的离心率的取值范围是( )
| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,2) | C. | (2,+∞) | D. | (1,2) |
13.已知f(x+1)是周期为2的奇函数,当-1≤x≤0时,f(x)=-2x(x+1),则f(-$\frac{3}{2}$)的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |