题目内容
7．在平面直角坐标系xOy中，双曲线中心在原点，焦点在y轴上，离心率为$\sqrt{5}$，则其渐进线方程为（ ）| A． | y=$\frac{1}{2}$x | B． | y=±$\frac{1}{2}$x | C． | y=-$\frac{1}{2}$x | D． | y=±2x |
分析 利用双曲线的离心率，求出a，b关系，然后求解渐近线方程．
解答 解：因为e=$\sqrt{5}$，所以$\frac{b}{a}=\sqrt{{e}^{2}-1}=2$，而焦点在y轴上的双曲线的渐进线方程为：y=$±\frac{a}{b}x$，
所以该双曲线的渐进线方程为：y=±$\frac{1}{2}$x．
故选：B．
点评 本题考查双曲线方程的简单性质的应用，基本知识的考查．
练习册系列答案
相关题目
如图，圆O中AB=4为直径，直线CE与圆O相切于点C，AD⊥CE于点D，若AD=1，∠ACD=θ，则cosθ=$\frac{\sqrt{3}}{2}$．
2．江苏舜天足球俱乐部为救助在“3.10云南盈江地震”中失学的儿童，准备在江苏省五台山体育场举行多场足球义赛，预计卖出门票2.4万张，票价分别为3元、5元和8元三种，且票价3元和5元的张数的积为0.6万张．设x是门票的总收入，经预算扣除其它各项开支后，该俱乐部的纯收入函数模型为y=lg2x，则当这三种门票的张数分别为（ ）万张时，可以为失学儿童募捐的纯收入最大．
| A． | 1、0．、0.8 | B． | 0.6、0.8、1 | C． | 0.6、1、0.8 | D． | 0.6、0.6、0.8 |
19．
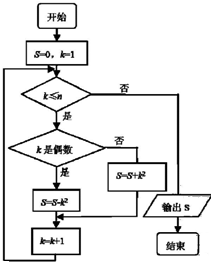阅读如图所示的程序框图，运行相应的程序，若输入n的值为100，则输出S的值为（ ）
阅读如图所示的程序框图，运行相应的程序，若输入n的值为100，则输出S的值为（ ）| A． | -1050 | B． | 5050 | C． | -5050 | D． | -4950 |
16．已知F1是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点，过F1且垂直于x轴的直线与双曲线交于A、B两点，E是双曲线的右顶点，若△ABE是钝角三角形，则该双曲线的离心率的取值范围是（ ）
| A． | （1，$\sqrt{3}$） | B． | （$\sqrt{3}$，2） | C． | （2，+∞） | D． | （1，2） |
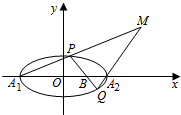如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右准线l的方程为x=$\frac{4\sqrt{3}}{3}$，焦距为2$\sqrt{3}$．