题目内容
【题目】设P={
}，Q={ 
} ，
，
（1）求
；
（2）若
，求a的取值范围．
【答案】(1) 
.
(2) (－1，
．
【解析】
（1）利用绝对值不等式的解法以及一元二次不等式的解法求解不等式组，即可得到集合
；(2)分类讨论，分别利用一元二次不等式的解法求解
，利用包含关系列不等式，从而可得
的取值范围.
（1）由
，得
由
，得
（2）［1，4］
有两种情况：
其一是Q=
，此时Δ＜0；
其二是Q≠，此时Δ=0或Δ＞0，
分三种情况计算a的取值范围．
设f(x)=x2 －2ax+a+2，
有Δ=(－2a)2－(4a+2)=4(a2－a－2)
当Δ＜0时，－1＜a＜2，Q= 
［1，4］；
当Δ=0时，a=－1或2；
若a=－1时Q={－1}不合要求；
若a=2时，Q={2}［1，4］．
当Δ＞0时，a＜－1或a＞2．
设方程f(x)=0的两根x1，x2，且x1＜x2，
那么Q=［x1，x2］，
Q［1，4］
1≤x1＜x2≤4
，
即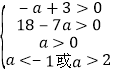
，解得2＜a
，
综上可知：
时，a的取值范围是(－1， ．
【题目】学校高三数学备课组为了更好地制定复习计划，开展了试卷讲评后效果的调研，从上学期期末数学试题中选出一些学生易错题，重新进行测试，并认为做这些题不出任何错误的同学为“过关”，出了错误的同学为“不过关”，现随机抽查了年级50人，他们的测试成绩的频数分布如下表：
期末分数段 |
|
|
|
|
|
|
人数 | 5 | 10 | 15 | 10 | 5 | 5 |
“过关”人数 | 1 | 2 | 9 | 7 | 3 | 4 |
（1）由以上统计数据完成如下
列联表，并判断是否有
的把握认为期末数学成绩不低于90分与测试“过关”有关？说明你的理由：
分数低于90分人数 | 分数不低于90分人数 | 合计 | |
“过关”人数 | |||
“不过关”人数 | |||
合计 |
（2）在期末分数段
的5人中，从中随机选3人，记抽取到过关测试“过关”的人数为
，求
的分布列及数学期望．
下面的临界值表供参考：
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
