Question

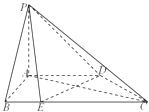
【题目】如图，在△ABC中，∠ABC=90°，AB= ，BC=1，P为△ABC内一点，∠BPC=90°

（1）若PB= ，求PA；
（2）若∠APB=150°，求tan∠PBA．

Answer 1

【答案】
（1）解：在△ABC中，由于AB= ，BC=1，P为△ABC内一点，∠BPC=90°，

直角三角形PBC中，若PB= ，∵cos∠PBC= = = ，∴∠PBC=60°．

∴∠PBA=∠ABC﹣∠PBC=90°﹣60°=30°．

在△PBA中，由余弦定理得PA2= = ，∴PA=

（2）解：设∠PBA=α，由已知得，PB=sinα，在△PBA中，由正弦定理得， ，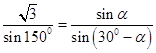

化简得， ，∴tanα= ，即tan∠PBA=

【解析】（Ⅰ）由题意利用直角三角形中的边角关系求得∠PBC=60°，∠PBA=∠ABC﹣∠PBC=30°．在△PBA中，由余弦定理求得PA的值．（Ⅱ）设∠PBA=α，由已知得，PB=sinα，在△PBA中，由正弦定理求得tanα的值．
【考点精析】通过灵活运用正弦定理的定义，掌握正弦定理:即可以解答此题．