题目内容
【题目】已知函数f(x)=|2x﹣1|+a|x﹣1|
(I)当a=1时,解关于x的不等式f(x)≥4
(II)若f(x)≥|x﹣2|的解集包含[ ![]() ,2],求实数a的取值范围.
,2],求实数a的取值范围.
【答案】解:(Ⅰ)当a=1时,f(x)=|2x﹣1|+|x﹣1|= 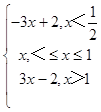 ,
,
∵f(x)≥4,
∴ 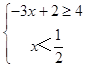 或
或 ![]() ,
,
解得x≤﹣ ![]() 或x≥2,
或x≥2,
故不等式的解集为(﹣∞,﹣ ![]() ]∪[2,+∞).
]∪[2,+∞).
(Ⅱ)∵f(x)≥|x﹣2|的解集包含[ ![]() ,2],
,2],
∴a|x﹣1|≥3﹣3x对x∈[ ![]() ,2]恒成立
,2]恒成立
当 ![]() ≤x<1时,a(1﹣x)≥3﹣3x,
≤x<1时,a(1﹣x)≥3﹣3x,
解得a≥3,
当1≤x≤2时,a(x﹣1)≥3﹣3x,
解得a≥﹣3,
综上:a≥3
【解析】(Ⅰ)由条件利用绝对值的意义求得不等式f(x)>4的解集.(Ⅱ)f(x)≥|x﹣2|的解集包含[ ![]() ,2],即为a|x﹣1|≥3﹣3x对x∈[
,2],即为a|x﹣1|≥3﹣3x对x∈[ ![]() ,2]恒成立,分类解得即可.
,2]恒成立,分类解得即可.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目






