��Ŀ����
����Ŀ��ij�����Ϊ���˽����¶�Ӫҵ���Ӱ���������¼�˸õ�1�·�����5�����Ӫҵ��y(��λ����Ԫ)��õص����������x(��λ����)�����������±���
![]()
(1)��y����x�����Իع鷽��![]() ��
��![]() x��
x��![]() ��
��
(2)�ж�y��x֮��������ػ��Ǹ���������õ�1�·�ij����������Ϊ6 ����������ع鷽��Ԥ��õ굱�յ�Ӫҵ�
(3)��õ�1�·ݵ����������X��N(������2)������������Ϊ����ƽ����![]() ����2����Ϊ��������s2����P(3.8��X��13.4)��
����2������������s2����P(3.8��X��13.4)��
�����ٻع鷽��![]() ����
����![]() ��
��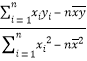 ��
��![]() =
=![]() ��
��![]() .
.
��![]() ��3.2��
��3.2��![]() ��1.8.��X��N(������2)����P(��������X��������)��0.682 7��P(����2����X������2��)��0.954 5.
��1.8.��X��N(������2)����P(��������X��������)��0.682 7��P(����2����X������2��)��0.954 5.
���𰸡�(1)![]() =��0.56x+12.92 (2) y��x֮���Ǹ���أ��õ굱�յ�Ӫҵ��ԼΪ9 560Ԫ��3��0.818 6
=��0.56x+12.92 (2) y��x֮���Ǹ���أ��õ굱�յ�Ӫҵ��ԼΪ9 560Ԫ��3��0.818 6
�������������������1�����ݱ������ݼ���![]() ��
��![]() ������ع�ϵ����д���ع鷽�̣�
������ع�ϵ����д���ع鷽�̣�
��2�����ݻع鷽�̵�б��Ϊ���ж�y��x֮���Ǹ���أ�����x=6ʱ![]() ��ֵ������
��ֵ������
(3) ��������s2��10����֪�������X��N(7,3.22)���Ӷ����P(3.8��X��13.4)��
���������
(1)![]() ��
��![]() ��(2��5��8��9��11)��7��
��(2��5��8��9��11)��7��
![]() ��
��![]() ��(1.2��1��0.8��0.8��0.7)��0.9.
��(1.2��1��0.8��0.8��0.7)��0.9.
![]() ��4��25��64��81��121��295��
��4��25��64��81��121��295��
![]() iyi��2.4��5��6.4��7.2��7.7��28.7��
iyi��2.4��5��6.4��7.2��7.7��28.7��
��![]() =
=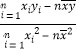 =
=![]() =��0.56��
=��0.56��
![]() ��
��![]() ��
��![]()
![]() ��0.9��(��0.056)��7��1.292.
��0.9��(��0.056)��7��1.292.
�����Իع鷽��Ϊ![]() ����0.056x��1.292.
����0.056x��1.292.
(2)��![]() ����0.056��0����y��x֮���Ǹ���أ�
����0.056��0����y��x֮���Ǹ���أ�
��x��6ʱ��![]() ����0.056��6��1.292��0.956.
����0.056��6��1.292��0.956.
��õ굱�յ�Ӫҵ��ԼΪ9 560Ԫ��
(3)��������s2��![]() ��(25��4��1��4��16)��10��
��(25��4��1��4��16)��10��
���������X��N(7,3.22)��
��P(3.8��X��10.2)��0.682 7��
P(0.6��X��13.4)��0.954 5��
��P(10.2��X��13.4)��![]() ��(0.954 5��0.682 7)��0.135 9.
��(0.954 5��0.682 7)��0.135 9.
��P(3.8��X��13.4)��P(3.8��X��10.2)��P(10.2��X��13.4)��0.682 7��0.135 9��0.818 6.






