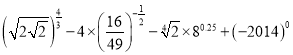Question

【题目】已知点F为抛物线C：x2＝2py (p＞0) 的焦点，点A(m，3)在抛物线C上，且|AF|＝5，若点P是抛物线C上的一个动点，设点P到直线的距离为，设点P到直线的距离为．

(1)求抛物线C的方程；

(2) 求的最小值；

(3)求的最小值．

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）根据抛物线的定义，将的长度转化为点纵坐标到准线的距离，从而得到，求出抛物线方程.

（2）将抛物线上点的到直线的距离转化为直线与抛物线相切时，两平行线之间的距离.

（3）利用抛物线定义，将转化为的长度，从而的值等于焦点到直线的距离，再求出其最小值.

（1）抛物线，

所以抛物线的准线为

由抛物线的定义得，，

解得，所以抛物线的方程为

（2）设直线的平行线：与抛物线相切，

整理得

得

故所求的最小值为

（3）由直线是抛物线的准线，

所以的最小值等于到直线的距离：

故所求的最小值为.