题目内容
【题目】已知圆
,直线
,若直线
上存在点
，过点引圆的两条切线
,使得
,则实数
的取值范围是（ ）
A. 
B. [
,
]
C. 
D. 
）
【答案】D
【解析】
由题意结合几何性质可知点P的轨迹方程为
，则原问题转化为圆心到直线的距离小于等于半径，据此求解关于k的不等式即可求得实数k的取值范围.
圆C（2,0），半径r＝
，设P（x，y），
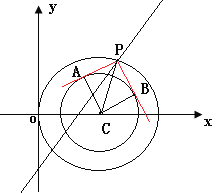
因为两切线
，如下图，PA⊥PB，由切线性质定理，知：
PA⊥AC，PB⊥BC，PA＝PB，所以，四边形PACB为正方形，所以，｜PC｜＝2，
则：，即点P的轨迹是以（2,0）为圆心，2为半径的圆.
直线
过定点（0，－2），直线方程即
，
只要直线与P点的轨迹（圆）有交点即可，即大圆的圆心到直线的距离小于等于半径，
即：
，解得：
，
即实数
的取值范围是
）.
本题选择D选项.
练习册系列答案
提分百分百检测卷系列答案
相关题目
