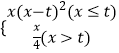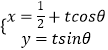��Ŀ����
����Ŀ��ij��������ͬ����һ�ֲ�Ʒ�����ݼ�������ϸ��Ʒ������y��g����ߴ�x��mm��֮����������ϵʽy=axb��a��bΪ����0�ij��������������ȡ6���ϸ��Ʒ������������£�
�ߴ磨mm�� | 38 | 48 | 58 | 68 | 78 | 88 |
������g�� | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
���������˳������������ͳ������ֵ�����
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
�������������ݣ���y����x�Ļع鷽�̣�
������ij��ָ��ⶨ������Ʒ������ߴ�ı������䣨 ![]() ��
�� ![]() ����ʱΪ�ŵ�Ʒ���ִӳ�ȡ��6���ϸ��Ʒ������ѡ3�����Ǧ�Ϊȡ���ŵ�Ʒ�ļ�����������������εķֲ��к�������
����ʱΪ�ŵ�Ʒ���ִӳ�ȡ��6���ϸ��Ʒ������ѡ3�����Ǧ�Ϊȡ���ŵ�Ʒ�ļ�����������������εķֲ��к�������
��������һ�����ݣ�v1 �� u1������v2 �� u2����������vn �� un������ع�ֱ��u=��+��v��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ ![]() =
= 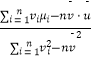 ��
�� ![]() =
= ![]() ��
�� ![]() ��
��
���𰸡��⣺����y=axb��a��b��0������ȡ��ѧ������lny=blnx+lna��
��vi=lnxi��ui=lnyi��u=bv+lna��
�� 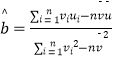 =
= ![]() ��
��
ln ![]() . =1��
. =1�� ![]() =e��
=e��
������ع鷽��Ϊ ![]() ��
��
������ 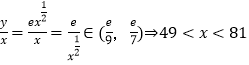 ��
��
58��68��78�����ŵ�Ʒ��3����
�εĿ���ȡֵ��0��1��2��3���� ![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��ֲ���Ϊ��
�� | 0 | 1 | 2 | 3 |
P |
|
|
|
|
�� ![]() ��
��
����������1����y=axb��a��b��0������ȡ��ѧ������lny=blnx+lna������vi=lnxi��ui=lnyi��u=bv+lna������С���˷����ϵ�� ![]() ,��������ع鷽�̣���2��������ó��εĿ���ȡֵ��0��1��2��3���ֱ���ø��ʣ��г��ֲ��У������ѧ����.
,��������ع鷽�̣���2��������ó��εĿ���ȡֵ��0��1��2��3���ֱ���ø��ʣ��г��ֲ��У������ѧ����.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�