Question

6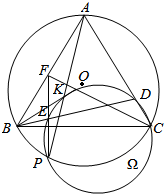．如图，△ABC内接于圆O，P为$\widehat{BC}$上一点，点K在线段AP上，使得BK平分∠ABC．过K，P，C三点的圆Ω与边AC交于点D，连接BD交圆Ω于点E，连接PE并延长与边AB交于点F．证明：∠ABC=2∠FCB．

Answer 1

分析 设CF与圆Ω交于L（异于点C），连结PB、PC、BL、KL，利用A、B、P、C四点共圆，推导出△FBE∽△FPB，再由切割线定理，得到FB²=FL•FC，从而推导出三点B、K、L共线，由此能证明∠ABC=2∠FCB．

解答 证明：设CF与圆Ω交于L（异于点C），连结PB、PC、BL、KL，
由题意，得此时C、D、L、K、E、P六点均在圆Ω上，
∵A、B、P、C四点共圆，∴∠FEB=∠DEP=180°-∠DCP=∠ABP=∠FBP，
∴△FBE∽△FPB，∴FB²=FE•FP，
由切割线定理，得FE•FP=FL•FC，
∴FB²=FL•FC，
∴△FBL∽△FCB，
∴∠FLB=∠FBC=∠APC=∠KPC=∠FLK，即三点B、K、L共线，
∵△FBL∽△FCB，∴∠FCB=∠FBL=∠FBE=$\frac{1}{2}∠ABC$，
∴∠ABC=2∠FCB．

点评 本题考查与圆有关的角相等的证明，是中档题，解题时要认真审题，注意四点共圆、三角形相似、切割线定理等知识点的合理运用．