题目内容
14.已知实数x,y满足x2+y2-xy+2x-y+1=0,求x,y的值.分析 x2+y2-xy+2x-y+1=0,可得4x2+4y2-4xy+8x-4y+4=0,变形为3(x2+2x+1)+(x2+4y2+2x-4xy-4y+1)=0,配方为3(x+1)2+(x-2y+1)2=0,即可得出.
解答 解:x2+y2-xy+2x-y+1=0,
∴4x2+4y2-4xy+8x-4y+4=0,
化为3(x2+2x+1)+(x2+4y2+2x-4xy-4y+1)=0,
即3(x+1)2+(x-2y+1)2=0,
∴$\left\{\begin{array}{l}{x+1=0}\\{x-2y+1=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$.
∴x=-1,y=0.
点评 本题考查了配方法、变形能力与计算能力,属于中档题.

练习册系列答案
相关题目
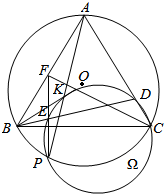 如图,△ABC内接于圆O,P为$\widehat{BC}$上一点,点K在线段AP上,使得BK平分∠ABC.过K,P,C三点的圆Ω与边AC交于点D,连接BD交圆Ω于点E,连接PE并延长与边AB交于点F.证明:∠ABC=2∠FCB.
如图,△ABC内接于圆O,P为$\widehat{BC}$上一点,点K在线段AP上,使得BK平分∠ABC.过K,P,C三点的圆Ω与边AC交于点D,连接BD交圆Ω于点E,连接PE并延长与边AB交于点F.证明:∠ABC=2∠FCB.