题目内容
18.已知函数f(x)对任意实数a、b,都有f(ab)=f(a)+f(b)成立.(1)求f(0)与f(1)的值;
(2)求证:f($\frac{1}{x}$)=-f(x);
(3)若f(2)=p,f(3)=q(p,q均为常数),求f(36)的值.
分析 (1)分别令a=b=0和a=b=1,即可求f(0)与f(1)的值;
(2)根据条件即可证明f($\frac{1}{x}$)=-f(x);
(3)根据抽象函数的关系进行转化即可求f(36)的值.
解答 解:(1)∵f(ab)=f(a)+f(b),
∴令a=b=0,则f(0)=f(0)+f(0),
即f(0)=0,
令a=b=1,
则f(1)=f(1)+f(1),
即f(1)=0;
证明:(2)∵$\frac{1}{x}$•x=1,
∴f($\frac{1}{x}$)+f(x)=f($\frac{1}{x}$•x)=f(1)=0,
则f($\frac{1}{x}$)=-f(x);
(3)若f(2)=p,f(3)=q(p,q均为常数),
则f(2)+f(3)=f(2×3)=f(6),
即f(6)=p+q,
则f(36)=f(6×6)=f(6)+f(6)=2f(6)=2p+2q.
点评 本题主要考查抽象函数的应用,利用赋值法是解决本题的关键.注意条件之间的转化和应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
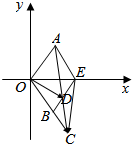 如图所示,△AOE和△BOE都是边长为1的等边三角形,延长OB到C,使|BC|=t|OB|(t>0),连接AC交BE于D,
如图所示,△AOE和△BOE都是边长为1的等边三角形,延长OB到C,使|BC|=t|OB|(t>0),连接AC交BE于D,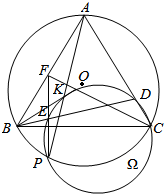 如图,△ABC内接于圆O,P为$\widehat{BC}$上一点,点K在线段AP上,使得BK平分∠ABC.过K,P,C三点的圆Ω与边AC交于点D,连接BD交圆Ω于点E,连接PE并延长与边AB交于点F.证明:∠ABC=2∠FCB.
如图,△ABC内接于圆O,P为$\widehat{BC}$上一点,点K在线段AP上,使得BK平分∠ABC.过K,P,C三点的圆Ω与边AC交于点D,连接BD交圆Ω于点E,连接PE并延长与边AB交于点F.证明:∠ABC=2∠FCB.