题目内容
16．已知f（x）=$\frac{1}{1+x}$（x∈R，且x≠-1），g（x）=x2+2（x∈R）．（1）求f（2），g（2）的值；
（2）求f（f（2）]的值；
（3）求f[g（x）]和g[f（x）]的解析式．
分析 （1）分别令x=2，代入即可求f（2），g（2）的值；
（2）先求出f（2），代入即可求f（f（2）]的值；
（3）分别代入即可求f[g（x）]和g[f（x）]的解析式．
解答 解：（1）∵f（x）=$\frac{1}{1+x}$（x∈R，且x≠-1），g（x）=x2+2（x∈R）．
∴f（2）=$\frac{1}{1+2}=\frac{1}{3}$，g（2）=22+2=4+2=6；
（2）∵f（2）=$\frac{1}{3}$，
∴f（f（2）]=f（$\frac{1}{3}$）=$\frac{1}{1+\frac{1}{3}}$=$\frac{3}{4}$；
（3）f[g（x）]=f（x2+2）=$\frac{1}{1+{x}^{2}+2}$=$\frac{1}{{x}^{2}+3}$，
g[f（x）]=g（$\frac{1}{1+x}$）=（$\frac{1}{1+x}$）2+2．
点评 本题主要考查函数解析式的应用，根据函数解析式直接代入是解决本题的关键．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
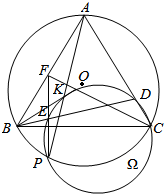如图，△ABC内接于圆O，P为$\widehat{BC}$上一点，点K在线段AP上，使得BK平分∠ABC．过K，P，C三点的圆Ω与边AC交于点D，连接BD交圆Ω于点E，连接PE并延长与边AB交于点F．证明：∠ABC=2∠FCB．