题目内容
已知数列{an}的前n项和Sn,求通项an.
(1)Sn=3n-1;
(2)Sn=n2+3n+1.
(1)Sn=3n-1;
(2)Sn=n2+3n+1.
(1)an=2·3n-1(2)an=

(1)n=1时,a1=S1=2.
n≥2时,an=Sn-Sn-1=2·3n-1.
当n=1时,an=1符合上式.
∴an=2·3n-1.
(2)n=1时,a1=S1=5.
n≥2时,an=Sn-Sn-1=2n+2.
当n=1时a1=5不符合上式.
∴an=
n≥2时,an=Sn-Sn-1=2·3n-1.
当n=1时,an=1符合上式.
∴an=2·3n-1.
(2)n=1时,a1=S1=5.
n≥2时,an=Sn-Sn-1=2n+2.
当n=1时a1=5不符合上式.
∴an=


练习册系列答案
相关题目
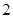 的等比数列
的等比数列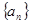 的各项都是正数,且
的各项都是正数,且 ,则
,则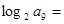 ( )
( )


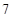
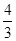 ,则{an}的前10项和等于( )
,则{an}的前10项和等于( )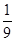 (1-310)
(1-310)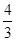 ,则{an}的前10项和为________.
,则{an}的前10项和为________.