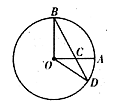题目内容
如图,在△ABC中,已知CM是∠ACB的平分线,△AMC的外接圆交BC于点N.若AC= AB,求证:BN=2AM.
AB,求证:BN=2AM.
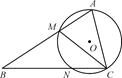
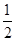 AB,求证:BN=2AM.
AB,求证:BN=2AM.
见解析
在△ABC中,因为CM是∠ACB的角平分线,所以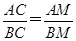 .
.
又已知AC=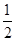 AB,所以
AB,所以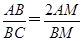 .①又BA与BC是圆O过同一点B的割线,
.①又BA与BC是圆O过同一点B的割线,
所以BM·BA=BN·BC,即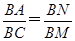 .②由①②可知,
.②由①②可知,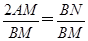 ,所以BN=2AM.
,所以BN=2AM.
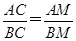 .
.又已知AC=
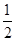 AB,所以
AB,所以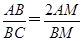 .①又BA与BC是圆O过同一点B的割线,
.①又BA与BC是圆O过同一点B的割线,所以BM·BA=BN·BC,即
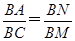 .②由①②可知,
.②由①②可知,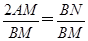 ,所以BN=2AM.
,所以BN=2AM.
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
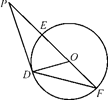
 CD.
CD.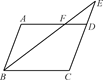
 是⊙
是⊙ 的直径
的直径 延长线上一点,
延长线上一点, 与⊙
与⊙ ,
, 的角平分线交
的角平分线交 于点
于点 ,则
,则 的大小为_________.
的大小为_________.
 为圆
为圆 的直径,
的直径, ,过圆
,过圆 作圆
作圆 ,过点
,过点 于点
于点 ,若
,若 中点,则
中点,则 =_____.
=_____.
 的直径
的直径 ,
, 为
为 ,过点
,过点 的
的 延长线于点
延长线于点 ,则
,则 ________;
________;
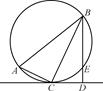
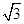 ,求圆O的半径长和∠EFD的大小.
,求圆O的半径长和∠EFD的大小.