题目内容
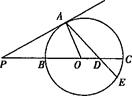
如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,求DE的长.

5
延长BA交切线CD于M.因为∠C=90°,
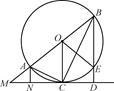
所以AB为直径,所以半径为10.连结OC,则OC⊥CD,且OC∥BD.
因为∠OAC=60°,所以∠AOC=60°,∠OBE=60°,
即BE=OB=10且∠M=30°.
所以OM=2OC=20,所以AM=10.
所以BD=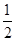 (AM+AB)=
(AM+AB)=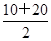 =15,
=15,
即DE=BD-BE=15-10=5.

所以AB为直径,所以半径为10.连结OC,则OC⊥CD,且OC∥BD.
因为∠OAC=60°,所以∠AOC=60°,∠OBE=60°,
即BE=OB=10且∠M=30°.
所以OM=2OC=20,所以AM=10.
所以BD=
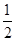 (AM+AB)=
(AM+AB)=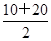 =15,
=15,即DE=BD-BE=15-10=5.

练习册系列答案
相关题目
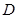 ,
,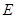 分别为
分别为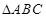 的边
的边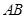 ,
,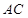 上的点,且不与
上的点,且不与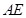 的长为
的长为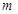 ,AC的长为n,
,AC的长为n,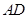 ,
,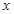 的方程
的方程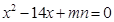 的两个根。
的两个根。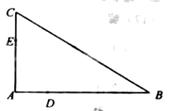
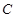 ,
,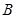 ,
,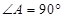 ,且
,且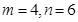 ,求
,求 AB,求证:BN=2AM.
AB,求证:BN=2AM.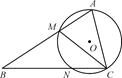

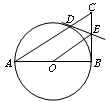
 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.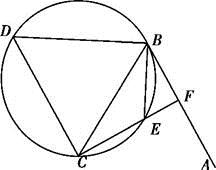
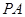 是⊙
是⊙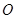 的切线,
的切线,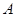 是切点,直线
是切点,直线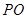 交⊙
交⊙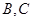 两点,
两点,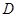 是
是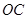 的中点,连接
的中点,连接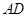 并延长交⊙
并延长交⊙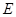 ,若
,若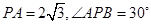 ,则
,则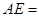 .
.