题目内容
【题目】已知函数 ![]()
![]() 在
在 ![]() 上单调递增,
上单调递增,
(1)若函数 ![]() 有实数零点,求满足条件的实数
有实数零点,求满足条件的实数 ![]() 的集合
的集合 ![]() ;
;
(2)若对于任意的 ![]() 时,不等式
时,不等式 ![]() 恒成立,求
恒成立,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:函数 ![]() 级
级 ![]() 单调递增区间是
单调递增区间是 ![]() ,因为
,因为 ![]() 在
在 ![]() 上单调递增,所以
上单调递增,所以 ![]() ;
;
令 ![]()
![]() ,则
,则 ![]()
![]()
函数 ![]() 有实数零点,即:
有实数零点,即: ![]() 在
在 ![]() 上有零点,只需:
上有零点,只需:
方法一 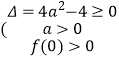 解得
解得 ![]()
方法二 ![]() 解得
解得 ![]()
综上: ![]() ,即
,即 ![]()
(2)解: ![]() 化简得
化简得 ![]()
因为对于任意的 ![]() 时,不等式
时,不等式 ![]() 恒成立,
恒成立,
即对于 ![]() 不等式
不等式 ![]() 恒成立,
恒成立,
设 ![]() (
( ![]() )
)
法一
当 ![]() 时,即
时,即 ![]() 不符合题意
不符合题意
当 ![]() 时,即
时,即 ![]() ,只需
,只需 ![]()
得 ![]() 从而
从而 ![]()
当 ![]() ,即
,即 ![]() ,只需
,只需 ![]()
得 ![]() 或
或 ![]() ,与
,与 ![]() 矛盾
矛盾
法二 ![]() 得
得 ![]()
综上知满足条件的 ![]() 的范围为
的范围为 ![]()
【解析】(1)首先根据二次函数对称轴的位置关系结合函数的增减性得到a的取值范围利用整体思想令 2x = t ( t > 0 )把原函数转化为f ( t ) = t 2 2 a t + 1 t > 0在 ( 0 , + ∞ ) 上有零点即在 ( 0 , + ∞ ) 上有根,结合二次函数图像的性质限制Δ≥0,a>0,f(0)>0得到关于a的不等式组解出即可。(2)结合(1)的结果整理化简不等式转化为当 1 ≤ a ≤ 2 不等式 ( 2x+1 1 ) a + 2 2x 2 > 0 恒成立,由整体思想构造函数 g(x) 关于2x 的二次函数当 1 ≤ a ≤ 2恒成立的问题,结合二次函数在指定区间上的最值问题解出x的取值范围即可。
【考点精析】认真审题,首先需要了解复合函数单调性的判断方法(复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”),还要掌握二次函数在闭区间上的最值(当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() )的相关知识才是答题的关键.
)的相关知识才是答题的关键.